题目内容
△ABC中,角A,B,C所对的边之长依次为a,b,c,且cosA=
,5(a2+b2-c2)=3
ab.
(Ⅰ)求cos2C和角B的值;
(Ⅱ)若a-c=
-1,求△ABC的面积.
2
| ||
| 5 |
| 10 |
(Ⅰ)求cos2C和角B的值;
(Ⅱ)若a-c=
| 2 |
考点:正弦定理,余弦定理
专题:解三角形
分析:(Ⅰ)利用已知5(a2+b2-c2)=3
ab代入余弦定理公式求得cosC的值,利用同角三角函数关系求得sinC的值,进而利用二倍角公式求得cos2C的值;通过cosA求得sinA的值,最后利用两角和公式取得sin(A+C)的值,进而取得sinB的值,求得B.
(Ⅱ)利用正弦定理求得a和c的关系式,代入a-c=
-1求得a和c,最后利用三角形面积公式求得答案.
| 10 |
(Ⅱ)利用正弦定理求得a和c的关系式,代入a-c=
| 2 |
解答:
解:(I)由∵cosA=
,0<A<π,
∴sinA=
=
,
∵5(a2+b2-c2)=3
ab,
∴cosC=
=
,
∵0<C<π,
∴sinC=
=
,
∴cos2C=2cos2C-1=
,
∴cosB=-cos(A+C)=-cosAcosC+sinAsinC=-
×
+
×
=-
∵0<B<π,
∴B=
.
(II)∵
=
,
∴a=
=
c,
∵a-c=
-1,
∴a=
,c=1,
∴S=
acsinB=
×
×1×
=
.
2
| ||
| 5 |
∴sinA=
| 1-cos2A |
| ||
| 5 |
∵5(a2+b2-c2)=3
| 10 |
∴cosC=
| a2+b2-c2 |
| 2ab |
3
| ||
| 10 |
∵0<C<π,
∴sinC=
| 1-cos2C |
| ||
| 10 |
∴cos2C=2cos2C-1=
| 4 |
| 5 |
∴cosB=-cos(A+C)=-cosAcosC+sinAsinC=-
2
| ||
| 5 |
3
| ||
| 10 |
| ||
| 5 |
| ||
| 10 |
| ||
| 2 |
∵0<B<π,
∴B=
| 3π |
| 4 |
(II)∵
| a |
| sinA |
| c |
| sinC |
∴a=
| csinA |
| sinC |
| 2 |
∵a-c=
| 2 |
∴a=
| 2 |
∴S=
| 1 |
| 2 |
| 1 |
| 2 |
| 2 |
| ||
| 2 |
| 1 |
| 2 |
点评:本题主要考查了正弦定理和余弦定理的综合运用,两角和与差的正弦公式等知识.考查学生对基础知识的综合运用.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
如图所示是一几何体的三视图,则该几何体的表面积为( )


| A、2 | ||||
B、
| ||||
C、4+
| ||||
D、4+
|
从6名教师中选4名开发A、B、C、D四门课程,要求每门课程有一名教师开发,每名教师只开发一门课程,且这6名中甲、乙两人不开发A课程,则不同的选择方案共有( )
| A、300种 | B、240种 |
| C、144种 | D、96种 |
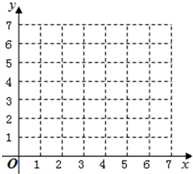 研究某设备的使用年限x与维修费用y之间的关系,测得一组数据如下(y值为观察值):
研究某设备的使用年限x与维修费用y之间的关系,测得一组数据如下(y值为观察值):