题目内容
设D={(x, y)|(x-y)(x+y)≤0},记“平面区域D夹在直线y=-1与y=t(t∈[-1,1])之间的部分的面积”为S,则函数S=f(t)的图象的大致形状为
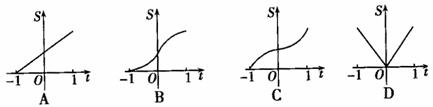
C

练习册系列答案
 导学与测试系列答案
导学与测试系列答案 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案
相关题目
题目内容
设D={(x, y)|(x-y)(x+y)≤0},记“平面区域D夹在直线y=-1与y=t(t∈[-1,1])之间的部分的面积”为S,则函数S=f(t)的图象的大致形状为
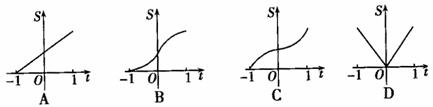
C

 导学与测试系列答案
导学与测试系列答案 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案