题目内容
已知f(x)=2cos2 +
+ sinwx+a的图象上相邻两对称轴的距离为
sinwx+a的图象上相邻两对称轴的距离为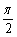 .
.
(1)若x∈R,求f(x)的递增区间;
(2)若x∈[0, 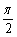 ]时,f(x)的最大值为4,求a的值。
]时,f(x)的最大值为4,求a的值。
解:已知f(x)= sinwx+coswx+a+1=2sin(wx+
sinwx+coswx+a+1=2sin(wx+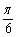 )+a+1
)+a+1
由 ,则T=π=
,则T=π= ,∴w=2
,∴w=2
∴f(x)=2sin(2x+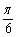 )+a+1
)+a+1
(1)令-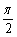 +2kπ≤2x+
+2kπ≤2x+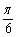 ≤
≤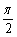 +2kπ
+2kπ
则-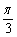 +kπ≤x≤
+kπ≤x≤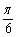 +kπ
+kπ
故f(x)的增区间是[kπ-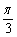 , kπ+
, kπ+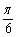 ], k∈Z
], k∈Z
(2)当x∈[0, 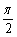 ]时,
]时,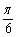 ≤2x+
≤2x+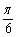 ≤
≤
∴sin(2x+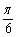 )∈[-
)∈[- , 1]
, 1]
∴fmax(x)=2+a+1=4, ∴a=1

练习册系列答案
相关题目
 的图象与函数g(x)=log2x图象交点个数是
的图象与函数g(x)=log2x图象交点个数是 ,则sin(α+
,则sin(α+ π)= 。
π)= 。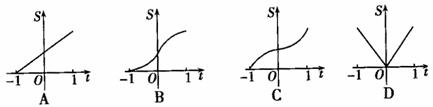
 ,
,  满足|
满足| |
| B.
B. C.
C.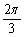 D.
D.
 B.
B. C.
C. D.
D.