题目内容
16.在极坐标系Ox中,Rt△OPQ的顶点O、P、Q按逆时针方向排列,∠OPQ=$\frac{π}{2}$,∠POQ=$\frac{π}{3}$,点P在曲线C1:ρ=2cosθ上运动(异于极点O).(1)当点P的极坐标为$({\sqrt{2},\frac{π}{4}})$,求点Q的极坐标;
(2)判断点Q的轨迹C2是何种曲线,并说明理由.
分析 (1)如图所示.当点P的极坐标为$({\sqrt{2},\frac{π}{4}})$,点Q的极径为2$\sqrt{2}$,极角为$\frac{π}{4}+\frac{π}{3}$.可得极坐标.
(2)点P在曲线C1:ρ=2cosθ上运动,∠OPQ=$\frac{π}{2}$,∠POQ=$\frac{π}{3}$,可得点Q的极坐标为$(4cosθ,θ+\frac{π}{3})$.可得x=4cosθ$cos(θ+\frac{π}{3})$,y=4cosθ$sin(θ+\frac{π}{3})$,θ∈$[-\frac{π}{2},\frac{π}{2})$.化简即可得出.
解答 解:(1)如图所示.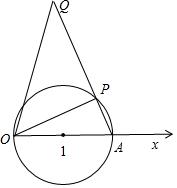 当点P的极坐标为$({\sqrt{2},\frac{π}{4}})$,
当点P的极坐标为$({\sqrt{2},\frac{π}{4}})$,
点Q的极坐标为$(2\sqrt{2},\frac{7π}{12})$.
(2)∵点P在曲线C1:ρ=2cosθ上运动,∠OPQ=$\frac{π}{2}$,∠POQ=$\frac{π}{3}$,
∴点Q的极坐标为$(4cosθ,θ+\frac{π}{3})$.
可得x=4cosθ$cos(θ+\frac{π}{3})$,y=4cosθ$sin(θ+\frac{π}{3})$,θ∈$[-\frac{π}{2},\frac{π}{2})$.
∴x2+y2=±2$(x+\sqrt{3}y)$,配方为:$(x+1)^{2}+(y+\sqrt{3})^{2}$=4,或$(x-1)^{2}+(y-\sqrt{3})^{2}$=4.
为两个圆.
点评 本题考查了极坐标方程化为直角坐标方程及其应用、直角三角形的边角关系,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 浙江之星课时优化作业系列答案
浙江之星课时优化作业系列答案 激活思维优加课堂系列答案
激活思维优加课堂系列答案
相关题目
7.对具有线性相关关系的变量x,y有一组观测数据(xi,yi)(i=1,2,3,…,n),观测数据均在回归直线方程$y=\frac{1}{3}x+2$上,则该组数据的残差平方和的值为( )
| A. | 0 | B. | $\frac{1}{3}$ | C. | 1 | D. | 2 |
11.某校从学生会文艺部6名成员(其中男生4人,女生2人)中,任选3人参加学校举办的“庆元旦迎新春”文艺汇演活动.设“男生甲被选中”为事件A,“女生乙被选中”为事件B,则P(B|A)为( )
| A. | $\frac{1}{5}$ | B. | $\frac{2}{5}$ | C. | $\frac{3}{5}$ | D. | $\frac{3}{10}$ |
1.圆心在(1,0)且过极点的圆的极坐标方程为( )
| A. | ρ=1 | B. | ρ=cos θ | C. | ρ=2cos θ | D. | ρ=2sin θ |
8.掷两枚均匀的大小不同的骰子,记“两颗骰子的点数和为8”为事件A,“小骰子出现的点数小于大骰子出现的点数”为事件B,则P(A|B),P(B|A)分别为( )
| A. | $\frac{2}{15},\frac{2}{5}$ | B. | $\frac{3}{14},\frac{3}{5}$ | C. | $\frac{1}{3},\frac{1}{5}$ | D. | $\frac{4}{5},\frac{4}{15}$ |