题目内容
16.已知抛物线的一个顶点为双曲线$\frac{{x}^{2}}{9}$-$\frac{{y}^{2}}{16}$=1的中心,抛物线的焦点在双曲线的焦点上,求此抛物线的方程.分析 求出双曲线的焦点坐标,然后求解抛物线方程.
解答 解:双曲线$\frac{{x}^{2}}{9}$-$\frac{{y}^{2}}{16}$=1的焦点坐标(5,0),(-5,0),
抛物线的一个顶点为双曲线$\frac{{x}^{2}}{9}$-$\frac{{y}^{2}}{16}$=1的中心,抛物线的焦点在双曲线的焦点上,
可得p=10,
所求的抛物线方程为:y2=±20x.
点评 本题考查抛物线的方程的求法,双曲线的简单性质的应用,抛物线的简单性质的应用,考查计算能力.

练习册系列答案
 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案
相关题目
6.设i是虚数单位,复数$\frac{a-i}{1+i}$(a∈R)的实部与虚部相等,则a=( )
| A. | -1 | B. | 0 | C. | 1 | D. | 2 |
7.已知a,b∈R,则使不等式|a+b|<|a|+|b|一定成立的条件是( )
| A. | a+b>0 | B. | a+b<0 | C. | ab>0 | D. | ab<0 |
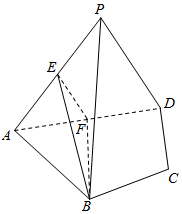 如图,在四棱锥P-ABCD中,平面PAD⊥平面ABCD,AB=AD,∠BAD=60°,E、F分别是AP、AD的中点.求证:
如图,在四棱锥P-ABCD中,平面PAD⊥平面ABCD,AB=AD,∠BAD=60°,E、F分别是AP、AD的中点.求证: