题目内容
2.若$f(x)=\frac{{sin(π-x)sin(\frac{3π}{2}+x)tan(π-x)}}{tan(x-π)sin(x-2π)}$,则函数f(x)的奇偶性为( )| A. | 偶函数 | B. | 奇函数 | ||
| C. | 既是奇函数又是偶函数 | D. | 既不是奇函数又不是偶函数 |
分析 利用诱导公式化简后,根据奇偶性的定义判断即可.
解答 解:$f(x)=\frac{{sin(π-x)sin(\frac{3π}{2}+x)tan(π-x)}}{tan(x-π)sin(x-2π)}$=$\frac{sinx•(-cosx)•(-tanx)}{tanx•sinx}$=cosx.
∵f(-x)=cos(-x)=cosx=f(x).
∴函数f(x)是偶函数.
故选:A.
点评 本题考查了诱导公式的化简能力和奇偶性的判断,属于基础题.

练习册系列答案
 一线名师提优试卷系列答案
一线名师提优试卷系列答案
相关题目
10.下列各式正确的是( )
| A. | tan(-$\frac{13}{4}$π)<tan(-$\frac{17}{5}$π) | B. | tan(-$\frac{13}{4}$π)>tan(-$\frac{17}{5}$π) | ||
| C. | tan(-$\frac{13}{4}$π)=tan(-$\frac{17}{5}$π) | D. | 大小关系不确定 |
11.设集合M={x|x2-2x-3≥0},N={x|-3<x<3},则( )
| A. | M⊆N | B. | N⊆M | C. | M∪N=R | D. | M∩N=∅ |
12.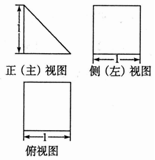 某几何体的三视图如图所示,则该几何体的体积为( )
某几何体的三视图如图所示,则该几何体的体积为( )
 某几何体的三视图如图所示,则该几何体的体积为( )
某几何体的三视图如图所示,则该几何体的体积为( )| A. | $\frac{1}{2}$ | B. | 1 | C. | $\frac{3}{2}$ | D. | 2 |
 是等比数列
是等比数列 的前
的前 项和,
项和, ,则此数列的公比
,则此数列的公比 ( )
( ) 或2 D.
或2 D. 或-1
或-1