题目内容
平面内共有7个点，其中有3个点共线，此外再无3点共线，则由这7个点可以构成的三角形有 个．
考点：排列、组合及简单计数问题
专题：排列组合
分析：利用间接法，平面内共有7个点，任取3个点，有
=35种方法，所取的3个点共线，有1种方法，即可得出由这7个点可以构成的三角形个数．
| C | 3 7 |
解答：
解：平面内共有7个点，任取3个点，有
=35种方法，
所取的3个点共线，有1种方法，
∴由这7个点可以构成的三角形个数为35-1=34个，
故答案为：34．
| C | 3 7 |
所取的3个点共线，有1种方法，
∴由这7个点可以构成的三角形个数为35-1=34个，
故答案为：34．
点评：本题考查计数原理的运用，考查学生的计算能力，比较基础．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
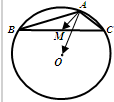如图，O为△ABC的外心，AB=6，AC=4，∠BAC为钝角，M是边BC的中点，则| AM |
| AO |
| A、-10 | B、36 | C、16 | D、13 |
已知实数a≥0，命题p，函数y=log2（x2+a）的定义域为R：命题q：x＞0是x≥a+1成立的必要条件但不是充分条件，则（ ）
| A、p∧q为真命题 |
| B、（￢p）∧q为真命题 |
| C、p∨q为假命题 |
| D、p∨（￢q）为真命题 |