题目内容
已知点M,N为圆C:x2+y2=9上的任意两点,且|MN|<2,若弦MN中点组成的区域为Ω,任意有序实数对(a,b)∈Ω,记函数f(x)=
ax2+bx+c在区间x∈(-1,1)上有且只有一个极小值点为事件A,则事件A发生的概率为 .
| ||
| 2 |
考点:利用导数研究函数的极值
专题:计算题,概率与统计
分析:先确定a2+b2=8,再确定-1<-
<1,且a>0,即可求出概率.
| b | ||
|
解答:
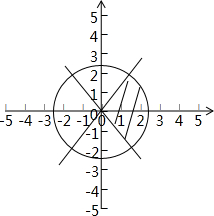 解:∵点M,N为圆C:x2+y2=9上的任意两点,且|MN|<2,若弦MN中点组成的区域为Ω,任意有序实数对(a,b)∈Ω,
解:∵点M,N为圆C:x2+y2=9上的任意两点,且|MN|<2,若弦MN中点组成的区域为Ω,任意有序实数对(a,b)∈Ω,
∴a2+b2=8.
∵f(x)=
ax2+bx+c,
∴f′(x)=
ax+b=0,
∵函数f(x)=
ax2+bx+c在区间x∈(-1,1)上有且只有一个极小值点,
∴-1<-
<1,且a>0,
对应的区域,如图所示阴影部分,两条直线的夹角为120°,
∴所求的概率为
.
故答案为:
.
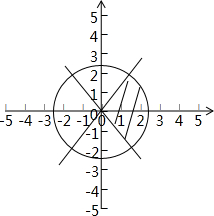 解:∵点M,N为圆C:x2+y2=9上的任意两点,且|MN|<2,若弦MN中点组成的区域为Ω,任意有序实数对(a,b)∈Ω,
解:∵点M,N为圆C:x2+y2=9上的任意两点,且|MN|<2,若弦MN中点组成的区域为Ω,任意有序实数对(a,b)∈Ω,∴a2+b2=8.
∵f(x)=
| ||
| 2 |
∴f′(x)=
| 3 |
∵函数f(x)=
| ||
| 2 |
∴-1<-
| b | ||
|
对应的区域,如图所示阴影部分,两条直线的夹角为120°,
∴所求的概率为
| 1 |
| 3 |
故答案为:
| 1 |
| 3 |
点评:本题考查利用导数研究函数的极值,考查概率知识,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目
函数y=3x+1的反函数是( )
| A、y=3x+1 | ||||
B、y=x-
| ||||
C、y=
| ||||
| D、y=3x-1 |
 一个多面体的直观图及三视图如图所示(其中M、N分别是AF、BC的中点),则多面体F-MNB的体积是
一个多面体的直观图及三视图如图所示(其中M、N分别是AF、BC的中点),则多面体F-MNB的体积是