题目内容
已知圆C过原点,圆心在射线y=2x(x>0)上,半径为
.
(1)求圆C的方程.
(2)若M为直线x+2y+5=0上的一动点,过M作圆C的切线,切点为A,求|MA|的最小值.
| 5 |
(1)求圆C的方程.
(2)若M为直线x+2y+5=0上的一动点,过M作圆C的切线,切点为A,求|MA|的最小值.
考点:直线和圆的方程的应用,圆的标准方程
专题:计算题,直线与圆
分析:(1)设圆C:(x-a)2+(y-b)2=r2,由条件列出方程,解出a,b即可;
(2)在直角三角形MAC中,|MA|2=|MC|2-|AC|2═|MC|2-5,要求|MA|的最小值,只要求|MC|的最小值,而C到直线x+2y+5=0的距离d即为|MC|的最小值.
(2)在直角三角形MAC中,|MA|2=|MC|2-|AC|2═|MC|2-5,要求|MA|的最小值,只要求|MC|的最小值,而C到直线x+2y+5=0的距离d即为|MC|的最小值.
解答:
 解:(1)设圆C:(x-a)2+(y-b)2=r2,
解:(1)设圆C:(x-a)2+(y-b)2=r2,
则a2+b2=r2①,b=2a②,r=
③(a>0)
解得a=1,b=2.
故圆C:(x-1)2+(y-2)2=5.
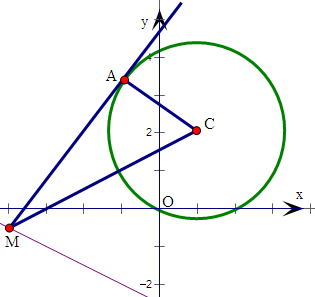
(2)如图,MA⊥AC,在直角三角形MAC中,
|MA|2=|MC|2-|AC|2═|MC|2-5,
要求|MA|的最小值,只要求|MC|的最小值,
而C到直线x+2y+5=0的距离d即为|MC|的最小值,由于d=
=2
,
则|MA|的最小值为
=
.
 解:(1)设圆C:(x-a)2+(y-b)2=r2,
解:(1)设圆C:(x-a)2+(y-b)2=r2,则a2+b2=r2①,b=2a②,r=
| 5 |
解得a=1,b=2.
故圆C:(x-1)2+(y-2)2=5.
(2)如图,MA⊥AC,在直角三角形MAC中,
|MA|2=|MC|2-|AC|2═|MC|2-5,
要求|MA|的最小值,只要求|MC|的最小值,
而C到直线x+2y+5=0的距离d即为|MC|的最小值,由于d=
| |1+2×2+5| | ||
|
| 5 |
则|MA|的最小值为
| 20-5 |
| 15 |
点评:本题考查圆的方程的求法,直线与圆的位置关系:相切,求切线长问题,考查几何法求最值的方法,是一道中档题.

练习册系列答案
相关题目