题目内容
已知O是△ABC所在平面内一点，D为BC边中点，
=
且λ
+
+
=
，则实数λ=（ ）
| AO |
| OD |
| OA |
| OB |
| OC |
| 0 |
| A、2 | ||
| B、-2 | ||
C、
| ||
D、-
|
考点：平面向量的基本定理及其意义
专题：平面向量及应用
分析：如图所示，由于D为BC边中点，可得
+
=2
，代入
=
且λ
+
+
=
，即可得出．
| OB |
| OC |
| OD |
| AO |
| OD |
| OA |
| OB |
| OC |
| 0 |
解答：
解：如图所示，
∵D为BC边中点，
∴
+
=2
，
∵
=
且λ
+
+
=
，
∴λ
+2
=
，
∴-λ
+2
=
，
∴λ=2．
故选：A．
∵D为BC边中点，
∴
| OB |
| OC |
| OD |
∵
| AO |
| OD |
| OA |
| OB |
| OC |
| 0 |
∴λ
| OA |
| OD |
| 0 |
∴-λ
| OD |
| OD |
| 0 |
∴λ=2．
故选：A．
点评：本题考查了向量的平行四边形法则、向量的线性运算、共面向量基本定理，考查了推理能力，属于基础题．
练习册系列答案
相关题目
如图，已知四棱锥的底面是边长为a的正方形，顶点在底面的射影是底面的中心，侧棱长为已知等差数列{an}中a3+a9+a15=9，则数列{an}的前17项和S17=（ ）
| A、102 | B、36 | C、48 | D、51 |
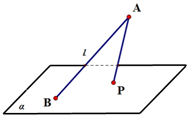如图，点A是平面α外一定点，过A作平面α的斜线l，斜线l与平面α所成角为50°．若点P在平面α内运动，并使直线AP与l所成角为35°，则动点P的轨迹是（ ）| A、圆 | B、椭圆 |
| C、抛物线 | D、双曲线的一支 |
函数f（x）=-x3-ax2+2bx（a，b∈R）在区间[-1，2]上单调递增，则
的取值范围是（ ）
| b |
| a |
| A、（-∞，-1）∪（2，+∞） |
| B、（2，+∞） |
| C、（-∞，-1） |
| D、（-1，2） |
△ABC的内角A、B、C的对边分别为a、b、c，若c=
，b=3，B=120°，则a等于（ ）
| 3 |
A、
| ||
| B、2 | ||
C、
| ||
D、
|