题目内容
函数f(x)=-x3-ax2+2bx(a,b∈R)在区间[-1,2]上单调递增,则
的取值范围是( )
| b |
| a |
| A、(-∞,-1)∪(2,+∞) |
| B、(2,+∞) |
| C、(-∞,-1) |
| D、(-1,2) |
考点:利用导数研究函数的单调性
专题:计算题,导数的综合应用
分析:先求出导函数,欲使函数f(x)在区间[1,2]上单调递增可转化成f′(x)≥0在区间[1,2]上恒成立,可得a,b满足的约束条件,利用线性规划知识可求
的取值范围.
| b |
| a |
解答:
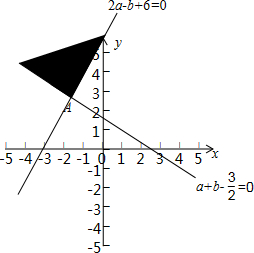 解:f′(x)=-3x2-2ax+2b,
解:f′(x)=-3x2-2ax+2b,
∵f(x)在[-1,2]上单调递增,
∴f′(x)≥0,即-3x2-2ax+2b≥0在[-1,2]上恒成立,
有
,即
,
则点(a,b)构成的区域如下图所示:
而
表示点(a,b)与原点连线的斜率,
由图可得
的取值范围是(-∞,-1)∪(2,+∞),
故选:A.
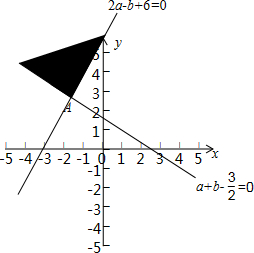 解:f′(x)=-3x2-2ax+2b,
解:f′(x)=-3x2-2ax+2b,∵f(x)在[-1,2]上单调递增,
∴f′(x)≥0,即-3x2-2ax+2b≥0在[-1,2]上恒成立,
有
|
|
则点(a,b)构成的区域如下图所示:
而
| b |
| a |
由图可得
| b |
| a |
故选:A.
点评:本题主要考查了利用导数研究函数的单调性,以及恒成立问题的转化,属于中档题.

练习册系列答案
 新编小学单元自测题系列答案
新编小学单元自测题系列答案 字词句段篇系列答案
字词句段篇系列答案
相关题目
已知定义在R上的函数f(x),则命题p:“f(-2)≠f(2)”是命题q:“y=f(x)不是偶函数”的( )
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
已知O是△ABC所在平面内一点,D为BC边中点,
=
且λ
+
+
=
,则实数λ=( )
| AO |
| OD |
| OA |
| OB |
| OC |
| 0 |
| A、2 | ||
| B、-2 | ||
C、
| ||
D、-
|
 (理)某几何体的三视图如图所示,若该几何体的外接球的表面积为3π,
(理)某几何体的三视图如图所示,若该几何体的外接球的表面积为3π,则正视图中a=( )
A、
| ||
B、
| ||
| C、2 | ||
| D、π |
不等式组
的解集用数轴表示为( )
|
A、 |
B、 |
C、 |
D、 |
一个等差数列的各项均不为0,且前4项是a,
,b,x,则
等于( )
| x |
| 2 |
| b |
| a |
A、
| ||
B、
| ||
| C、3 | ||
| D、2 |