题目内容
16.已知对于圆x2+y2-2y=0上任意一点P,不等式x+y+m≥0恒成立,则实数m的取值范围为( )| A. | m≥-1 | B. | m≥$\sqrt{2}$-1 | C. | m≤-$\sqrt{2}$-1 | D. | m≥$\sqrt{2}-1或m≤-\sqrt{2}$-1 |
分析 方法一、由圆的方程找出圆心坐标和半径,依题意得,只要圆上的点都在直线之上,临界情况就是直线和圆下部分相切,即圆心(0,1)到直线的距离是1,利用点到直线的距离公式得到关于m的方程,求出方程的解,根据图象判断符合题意的m的值即可得到使不等式恒成立时m的取值范围.
方法二、先设x=cosα,y-1=sinα,再把不等式x+y+m≥0恒成立转化为m≥-(x+y)恒成立,进而利用辅助角公式求-(x+y)的最小值即可得到结论.
解答  解:法一、圆的标准方程x2+(y-1)2=1得,圆心(0,1),半径r=1
解:法一、圆的标准方程x2+(y-1)2=1得,圆心(0,1),半径r=1
令圆x2+(y-1)2=1与直线x+y+m=0相切,
则圆心到直线的距离d=r,即 $\frac{|1+m|}{\sqrt{1+1}}$=1,化简得1+m=±$\sqrt{2}$,
即m=$\sqrt{2}$-1,m=-$\sqrt{2}$-1(舍去),
结合图象可知,当m≥$\sqrt{2}$-1时,圆上的任一点都能使不等式x+y+m≥0恒成立.
法二、由题设:x=cosα,y-1=sinα,
则 x+y=cosα+sinα+1=$\sqrt{2}$sin(α+$\frac{π}{4}$)+1∈[-$\sqrt{2}$+1,$\sqrt{2}$+1].
∵不等式x+y+m≥0恒成立
∴m≥-(x+y)恒成立;
因为-(x+y)的最大值为:$\sqrt{2}$-1.
∴m≥$\sqrt{2}$-1.
故选:B.
点评 本题考查直线与圆的关系,考查转化思想,学生掌握不等式恒成立时所满足的条件及直线与圆相切时所满足的条件,灵活运用点到直线的距离公式化简取值,灵活运用数形结合的数学思想解决实际问题,是一道综合题.本题也可以利用三角函数换元法进行求最值.

练习册系列答案
相关题目
6.f(x)为定义在R上的奇函数,当x>0时,f(x)=lnx,则f(x)>0的解集为( )
| A. | (1,+∞) | B. | (0,1)∪(1,+∞) | C. | (-1,0)∪(1,+∞) | D. | (-∞,-1)∪(1,+∞) |
7.函数f(x)=$\frac{1}{x^2-x}$+$\sqrt{2-x}$的定义域是( )
| A. | (-∞,1)∪(1,2) | B. | (-∞,0)∪(0,1)∪(1,2) | C. | (-∞,0)∪(1,2) | D. | (-∞,0)∪(0,1)∪(1,2] |
4.若实数x,y满足不等式组$\left\{\begin{array}{l}x+y≤1\\ x-y≤1\\ x≥0\end{array}\right.$,则2x+y的最大值是( )
| A. | -1 | B. | 0 | C. | 1 | D. | 2 |
1.已知函数f(x)是R上的增函数,A(0,-3),B(3,1)是其图象上的两点,那么不等式-3<f(x+1)<1的解集的补集是( )
| A. | (-1,2) | B. | (1,4) | C. | (-∞,-1)∪[4,+∞) | D. | (-∞,-1]∪[2,+∞) |
8.把复数z的共轭复数记作$\overline z$,i为虚数单位,若z=1+i,则(2+z)•$\overline z$=( )
| A. | 4+2i | B. | 4-2i | C. | 2+4i | D. | 4 |
5.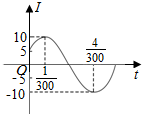 电流强度I(安)随时间t(秒)变化的函数I=Asin(ωt+φ)(A>0,ω>0,0<φ<$\frac{π}{2}$)的图象如右图所示,则当t=$\frac{1}{100}$秒时,电流强度是( )
电流强度I(安)随时间t(秒)变化的函数I=Asin(ωt+φ)(A>0,ω>0,0<φ<$\frac{π}{2}$)的图象如右图所示,则当t=$\frac{1}{100}$秒时,电流强度是( )
 电流强度I(安)随时间t(秒)变化的函数I=Asin(ωt+φ)(A>0,ω>0,0<φ<$\frac{π}{2}$)的图象如右图所示,则当t=$\frac{1}{100}$秒时,电流强度是( )
电流强度I(安)随时间t(秒)变化的函数I=Asin(ωt+φ)(A>0,ω>0,0<φ<$\frac{π}{2}$)的图象如右图所示,则当t=$\frac{1}{100}$秒时,电流强度是( )| A. | -5 A | B. | 5A | C. | 5$\sqrt{3}$ A | D. | 10 A |
6.已知抛物线M:y2=4x,圆N:(x-1)2+y2=r2(其中r为常数,r>0).过点(1,0)的直线l交圆N于C、D两点,交抛物线M于A、B两点,且满足|AC|=|BD|的直线l只有三条,则( )
| A. | r∈(0,1] | B. | r∈(1,$\frac{3}{2}$] | C. | r∈($\frac{3}{2}$,2] | D. | r∈(2,+∞) |