题目内容
15．在圆C：（x-2）2+（y-2）2=8内，过点P（1，1）的最长的弦为AB，最短的弦为DE，则四边形ADBE的面积为（ ）| A． | 2$\sqrt{3}$ | B． | 4$\sqrt{3}$ | C． | 8$\sqrt{3}$ | D． | 16$\sqrt{3}$ |
分析 由圆的知识可知过（1，1）的最长弦为直径，最短弦为过（1，1）且垂直于该直径的弦，然后利用对角线垂直的四边形的面积等于对角线乘积的一半求出即可．
解答 解：圆的标准方程为（x-2）2+（y-2）2=8，
由题意得最长的弦|AB|=4$\sqrt{2}$，
圆心（2，2），圆心与点（1，1）的距离d=$\sqrt{2}$，
根据勾股定理得最短的弦|DE|=2$\sqrt{6}$，且AB⊥DE，
四边形ABCD的面积S=$\frac{1}{2}$|AB|•|DE|=$\frac{1}{2}$×4$\sqrt{2}$×2$\sqrt{6}$=8$\sqrt{3}$，
故选：C．
点评 本题考查学生灵活运用几何知识决数学问题的能力，掌握对角线垂直的四边形的面积计算方法为对角线乘积的一半是解决问题的关键，属中档题．
练习册系列答案
相关题目
5．
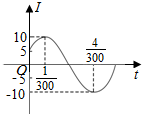电流强度I（安）随时间t（秒）变化的函数I=Asin（ωt+φ）（A＞0，ω＞0，0＜φ＜$\frac{π}{2}$）的图象如右图所示，则当t=$\frac{1}{100}$秒时，电流强度是（ ）
电流强度I（安）随时间t（秒）变化的函数I=Asin（ωt+φ）（A＞0，ω＞0，0＜φ＜$\frac{π}{2}$）的图象如右图所示，则当t=$\frac{1}{100}$秒时，电流强度是（ ）| A． | -5 A | B． | 5A | C． | 5$\sqrt{3}$ A | D． | 10 A |
6．已知抛物线M：y2=4x，圆N：（x-1）2+y2=r2（其中r为常数，r＞0）．过点（1，0）的直线l交圆N于C、D两点，交抛物线M于A、B两点，且满足|AC|=|BD|的直线l只有三条，则（ ）
| A． | r∈（0，1] | B． | r∈（1，$\frac{3}{2}$] | C． | r∈（$\frac{3}{2}$，2] | D． | r∈（2，+∞） |
20．已知函数f（x）=x2-2x，则下列各点中不在函数图象上的是（ ）
| A． | （1，-1） | B． | （-1，3） | C． | （2，0） | D． | （-2，6） |
4．某场排球赛决赛将在甲队与乙队之间展开，据以往统计，甲队在每局比赛中胜乙队的概率为$\frac{2}{3}$，比赛采取五局三胜制，即谁先胜三局谁就获胜，并停止比赛，则甲队以3：1获胜的概率为（ ）
| A． | $\frac{2}{3}$ | B． | $\frac{8}{27}$ | C． | $\frac{2}{9}$ | D． | $\frac{8}{9}$ |