题目内容
已知命题p:?x0∈R,x0n+a1x0n-1+a2x0n-2+…+an≤0,则( )
| A、¬p:?x∈R,xn+a1xn-1+a2xn-2+…+an≤0 |
| B、¬p:?x0∈R,x0n+a1x0n-1+a2x0n-2+…+an>0 |
| C、¬p:?x∈R,xn+a1xn-1+a2xn-2+…+an>0 |
| D、¬p:?x0∈R,x0n+a1x0n-1+a2x0n-2+…+an≥0 |
考点:命题的否定
专题:简易逻辑
分析:直接利用特称命题的否定是全称命题写出结果判断即可.
解答:
解:因为特称命题的 否定是全称命题.
所以,命题p:?x0∈R,x0n+a1x0n-1+a2x0n-2+…+an≤0,则¬p:?x∈R,xn+a1xn-1+a2xn-2+…+an>0.
故选:C.
所以,命题p:?x0∈R,x0n+a1x0n-1+a2x0n-2+…+an≤0,则¬p:?x∈R,xn+a1xn-1+a2xn-2+…+an>0.
故选:C.
点评:本题考查命题的否定,特称命题与全称命题的否定关系,基本知识的考查.

练习册系列答案
相关题目
向量
=(1,2),
=(-2,6),则
•
等于( )
| a |
| b |
| a |
| b |
| A、4 | B、6 | C、8 | D、10 |
已知向量
=(3,2),
=(-1,2),
=(4,1),若
+k
与2
-
共线,则k的值是( )
| a |
| b |
| c |
| a |
| c |
| b |
| a |
A、-
| ||
B、
| ||
C、-
| ||
D、
|
化简
可得( )
| log38 |
| log32 |
| A、log34 | ||
B、
| ||
| C、3 | ||
| D、4 |
两直线ax-y+2a=0和(2a-1)x+ay+a=0互相垂直,则a=( )
| A、1 | ||||
B、-
| ||||
| C、1或0 | ||||
D、-
|
若复数z满足(3-4i)z=|4+3i|,则z的虚部为( )
| A、-4 | ||
B、-
| ||
C、
| ||
| D、4 |
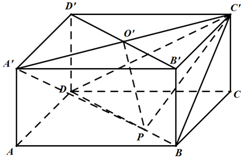 如图,在长方体ABCD-A′B′C′D′中,DA=DC=2,DD′=1,A′C′与B′D′相交于点O′,点P在线段BD上(点P与点B不重合).
如图,在长方体ABCD-A′B′C′D′中,DA=DC=2,DD′=1,A′C′与B′D′相交于点O′,点P在线段BD上(点P与点B不重合). 如图,在矩形ABCD中,AB=4,BC=3,沿对角线BD将Rt△ABD折起,使点A到P点,且点P在平面BCD内的射影O恰好落在CD边上,求二面角P-BD-C的正弦值.
如图,在矩形ABCD中,AB=4,BC=3,沿对角线BD将Rt△ABD折起,使点A到P点,且点P在平面BCD内的射影O恰好落在CD边上,求二面角P-BD-C的正弦值.