题目内容
8.已知数列{an}满足an=an-1+an-2(n>2),且a2015=1,a2017=-1,设{an}的前n项和为Sn,则S2020-S2016=( )| A. | -17 | B. | -15 | C. | -6 | D. | 0 |
分析 由递推式,可得a2016,a2018,a2019,a2020,而S2020-S2016=a2017+a2018+a2019+a2020,代入计算即可得到结果.
解答 解:∵an=an-1+an-2(n>2),a2015=1,a2017=-1,
∴a2017=a2016+a2015,
∴a2016=-2,a2018=-2-1=-3,a2019=-1-3=-4,a2020=-3-4=-7,
∴S2020-S2016=a2017+a2018+a2019+a2020=-1-3-4-7=-15.
故选:B.
点评 本题考查数列的求和,注意运用递推式,考查运算能力,属于基础题.

练习册系列答案
相关题目
20.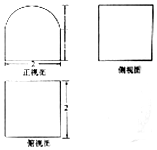 某个几何体的三视图如图(其中正视图中的圆弧是半圆)所示,则该几何体的表面积为( )
某个几何体的三视图如图(其中正视图中的圆弧是半圆)所示,则该几何体的表面积为( )
 某个几何体的三视图如图(其中正视图中的圆弧是半圆)所示,则该几何体的表面积为( )
某个几何体的三视图如图(其中正视图中的圆弧是半圆)所示,则该几何体的表面积为( )| A. | 12+3π | B. | 10+3π | C. | 12+4π | D. | 10+4π |
1.已知函数f(x)=$\left\{\begin{array}{l}{2^x},x<2\\ f(x-1),x≥2\end{array}\right.$则f(log27)=$\frac{7}{2}$.
18.已知a,b是两条不同的直线,α是平面,且b?α,那么“a∥α”是“a∥b”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
3.如果函数y=logax(a>0且a≠1)在[1,3]上的最大值与最小值的差为2,则满足条件的a值的集合是( )
| A. | $\{\sqrt{3}\}$ | B. | $\{\frac{{\sqrt{3}}}{3}\}$ | C. | $\{\frac{{\sqrt{3}}}{3},\sqrt{3}\}$ | D. | $\{\sqrt{3},3\}$ |
17.已知命题p:函数y=lg(1-x)在(-∞,1)上单调递减,命题q:函数y=2cosx是偶函数,则下列命题中为真命题的是( )
| A. | p∧q | B. | (¬p)∨(¬q) | C. | (¬p)∧q | D. | p∧(¬q) |
18.若(2x+1)n=a0+a1x+a2x2+…+anxn的展开式中的各项系数和为243,则a1+2a2+…+nan=( )
| A. | 405 | B. | 810 | C. | 243 | D. | 64 |
 如图古铜钱外圆内方,外圆直径为4cm,中间是边长为1cm的正方形孔,随机地在古铜钱所在圆内任取一点,则该点刚好位于孔中的概率是$\frac{1}{4π}$.
如图古铜钱外圆内方,外圆直径为4cm,中间是边长为1cm的正方形孔,随机地在古铜钱所在圆内任取一点,则该点刚好位于孔中的概率是$\frac{1}{4π}$.