题目内容
如果sinα+cosα=
,那么sinα-cosα的值为 .
| 3 |
| 4 |
考点:三角函数的化简求值
专题:三角函数的求值
分析:对sinα+cosα=
,两端平方可求得2sinαcosα=-
,于是可求得(sinα-cosα)2=1+
=
,再开方即可.
| 3 |
| 4 |
| 7 |
| 16 |
| 7 |
| 16 |
| 23 |
| 16 |
解答:
解:∵sinα+cosα=
,
∴(sinα+cosα)2=
,
∴1+2sinαcosα=
,
解得:2sinαcosα=-
;
令t=sinα-cosα,
则t2=(sinα-cosα)2=1+
=
,
∴t=±
,即sinα-cosα=±
.
故答案为:±
.
| 3 |
| 4 |
∴(sinα+cosα)2=
| 9 |
| 16 |
∴1+2sinαcosα=
| 9 |
| 16 |
解得:2sinαcosα=-
| 7 |
| 16 |
令t=sinα-cosα,
则t2=(sinα-cosα)2=1+
| 7 |
| 16 |
| 23 |
| 16 |
∴t=±
| ||
| 4 |
| ||
| 4 |
故答案为:±
| ||
| 4 |
点评:本题考查三角函数间的化简求值,考察二倍角的正弦的应用,属于中档题.

练习册系列答案
 活力课时同步练习册系列答案
活力课时同步练习册系列答案
相关题目
△ABC的三个内角A,B,C所对的分别为a,b,c,若
=
=
,则角C的大小为( )
| cosA |
| cosB |
| b |
| a |
| 2 |
| A、60° | B、75° |
| C、90° | D、120° |
已知曲线
+
=1(m<6)与曲线
+
=1(5<m<9),则两曲线的( )
| x2 |
| 10-m |
| y2 |
| 6-m |
| x2 |
| 5-m |
| y2 |
| 9-m |
| A、顶点相同 | B、焦点相同 |
| C、焦距相等 | D、离心率相等 |
设条件p:
≥0条件(x-1)(x+2)≥0.则p是q的( )
| x-1 |
| x+2 |
| A、充要条件 |
| B、必要不充分条件 |
| C、充分不必要条件 |
| D、既不充分也不必要条件 |
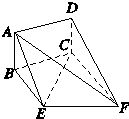 如图,矩形ABCD和梯形BEFC所在平面互相垂直,∠BCF=∠CEF=90°,AD=
如图,矩形ABCD和梯形BEFC所在平面互相垂直,∠BCF=∠CEF=90°,AD=