题目内容
15.已知函数f(x)=ex-kx,x∈R.(1)若k=e,试确定函数f(x)的单调区间和极值;
(2)若f(x)在区间[0,2]上单调递增,求实数k的取值范围.
分析 (1)利用导数与单调性、极值的关系求解:(2)f(x)在区间[0,2]上单调递增⇒f′(x)≥0上[0,2]恒成立.
解答 解:(Ⅰ)由 k=e得f(x)=ex-ex,所以 f′(x)=ex-e.…2分
令f′(x)=0 解得 x=1,
f′(x)与f(x)的关系如下表:
| x | (-∞,1) | 1 | (1,+∞) |
| f′(x) | _ | 0 | + |
| f(x) | 单减 | 单增 |
当 x=1时f(x) 取得极小值为 f(1)=0…..8分
(Ⅱ)若 f(x)在区间[0,2]上单调递增,则有
在 f′(x)=ex-k≥0上[0,2]恒成立,即 k≤ex,….…..10分
而 ex在[0,2]上的最小值为 1,
故 k≤1…12分
点评 本题考查了利用导数求单调区间、极值,考查了已知单调性求参数问题.

练习册系列答案
 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案
相关题目



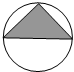
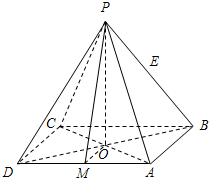 如图所示,四棱锥P-ABCD中,PA=PB=PC=PD,AB=a,O为底面正方形的中心,侧棱PA与底面ABCD所成的角的正切值为$\frac{{\sqrt{6}}}{2}$.
如图所示,四棱锥P-ABCD中,PA=PB=PC=PD,AB=a,O为底面正方形的中心,侧棱PA与底面ABCD所成的角的正切值为$\frac{{\sqrt{6}}}{2}$.