题目内容
16.已知向量$\overrightarrow{a}$=($\sqrt{3}$cosωx,1),$\overrightarrow{b}$=(sinωx,cos2ωx-$\frac{1}{2}$)(ω>0),函数f(x)=$\overrightarrow{a}•\overrightarrow{b}$,若函数f(x)的图象的一条对称轴与它相邻的一个对称中心的距离为$\frac{π}{4}$.(1)求f(x)的表达式;
(2)将函数f(x)的图象向右平移$\frac{π}{4}$个单位,再将各点的横坐标缩短到原来的$\frac{1}{2}$(纵坐标不变),得到函数y=g(x)的图象,求函数g(x)在区间$[0,\frac{π}{4}]$上的最大值和最小值.
分析 (1)利用向量的数量积公式,结合二倍角、辅助角公式,根据函数f(x)图象的一个对称中心与它相邻的一条对称轴之间的距离为$\frac{π}{4}$,即可求函数f(x)的解析式.
(2)根据图象的平移和正弦函数的图象的性质即可得出结论.
解答 解:(1)$f(x)=\sqrt{3}sinωxcosωx+{cos^2}ωx-\frac{1}{2}$=$\frac{{\sqrt{3}}}{2}sin2ωx+\frac{cos2ωx+1}{2}-\frac{1}{2}$.
由题意知f(x)的最小正周期T=$\frac{2π}{2ω}$=$\frac{π}{ω}$=π,所以ω=1,
所以f(x)=sin(2x+$\frac{π}{6}$).
(2)将f(x)的图象向右平移$\frac{π}{4}$个单位后,得到y=sin[2(x-$\frac{π}{4}$)+$\frac{π}{4}$]=sin(2x-$\frac{π}{3}$)
的图象,再将所得图象上所有点的横坐标缩短到原来的$\frac{1}{2}$,纵坐标不变,得到$y=sin(4x-\frac{π}{3})$的图象,
所以g(x)=sin(4x-$\frac{π}{3}$),
因为$0≤x≤\frac{π}{4}$,所以$-\frac{π}{3}≤4x-\frac{π}{3}≤\frac{2π}{3}$.由正弦函数的图象得可知$-\frac{{\sqrt{3}}}{2}≤g(x)≤1$.
所以g(x)在区间$[0,\frac{π}{4}]$上最大值为1和最小值为$-\frac{{\sqrt{3}}}{2}$.
点评 本题主要考查了函数y=Asin(ωx+φ)的图象变换,三角函数恒等变换的应用,周期公式,正弦函数的图象和性质,考查了计算能力和转化思想,属于中档题.

 习题精选系列答案
习题精选系列答案| A. | 30° | B. | 90° | C. | 60° | D. | 120° |



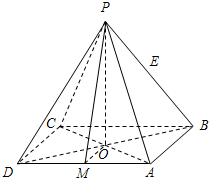 如图所示,四棱锥P-ABCD中,PA=PB=PC=PD,AB=a,O为底面正方形的中心,侧棱PA与底面ABCD所成的角的正切值为$\frac{{\sqrt{6}}}{2}$.
如图所示,四棱锥P-ABCD中,PA=PB=PC=PD,AB=a,O为底面正方形的中心,侧棱PA与底面ABCD所成的角的正切值为$\frac{{\sqrt{6}}}{2}$.