题目内容
2.若关于x的方程mx2+(m-1)x+m=0没有实数根,则实数m的取值范围是$(-∞,-1)∪(\frac{1}{3},+∞)$.分析 由题意可得它的判别式△=(1-m)2-4m•m<0,且m≠0,由此求得m的取值范围.
解答 解:由于关于x的一元二次方程mx2+(m-1)x+m=0没有实数根,
故它的判别式△=(1-m)2-4m•m<0,且m≠0,
求得m>$\frac{1}{3}$或m<-1,
故m的范围为(-∞,-1)∪($\frac{1}{3}$,+∞).
故答案为:$(-∞,-1)∪(\frac{1}{3},+∞)$.
点评 本题主要考查一元二次方程根的分布情况,考查运算能力,属于基础题.

练习册系列答案
 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案
相关题目
13.正四棱锥的顶点都在同一球面上,若该棱锥的高为4,底面边长为2,则该球的体积为( )
| A. | $\frac{243π}{16}$ | B. | $\frac{81π}{16}$ | C. | $\frac{81π}{4}$ | D. | $\frac{27π}{4}$ |
17.如果集合A={x|ax2+4x+1=0}中只有一个元素,则a的值是( )
| A. | 0 | B. | 4 | C. | 0 或4 | D. | 不能确定 |
7.三棱锥A-BCD,顶点A在平面BCD内的射影为O,若AB=AC=AD,则点O为△BCD的( )
| A. | 内心 | B. | 外心 | C. | 中心 | D. | 垂心 |
14.已知扇形OAB的面积为1,周长为4,则弦AB的长度为( )
| A. | 2 | B. | $\frac{2}{sin1}$ | C. | 2sin1 | D. | sin2 |
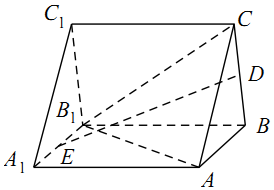 在如图所示的直三棱柱ABC-A1B1C1中,D,E分别是BC,A1B1的中点.
在如图所示的直三棱柱ABC-A1B1C1中,D,E分别是BC,A1B1的中点.