题目内容
 已知f(x)是定义在R上的偶函数,如图所示,线段OA,AB,BC和射线CD组成的折线是函数f(x)的部分图象,其中O为坐标原点,A(2,1),B(3,1),C(4,0),D(5,1).
已知f(x)是定义在R上的偶函数,如图所示,线段OA,AB,BC和射线CD组成的折线是函数f(x)的部分图象,其中O为坐标原点,A(2,1),B(3,1),C(4,0),D(5,1).(Ⅰ)求f(-1)和f(6)的值;
(Ⅱ)若f(log2x-1)>f(log2x),求实数x的取值范围.
考点:函数奇偶性的性质
专题:函数的性质及应用
分析:(1)先求出x∈[0,1],[4,+∞)的解析式,根据偶函数的性质求解,f(-1)=f(1).
(2)因为log2x-1<log2x,再由f(log2x-1)>f(log2x),得出函数是减函数,有偶函数和图象可得.
(2)因为log2x-1<log2x,再由f(log2x-1)>f(log2x),得出函数是减函数,有偶函数和图象可得.
解答:
解:当0≤x≤2时,可求得f(x)=
x,
因为f(x)是r上的偶函数,
所以f(-1)=f(1)=
,
又C(4,0)D(5,1),结合图形可求得:
当x≥4时,f(x)=x-4,
故f(6)=6-4=2
(2)∵log2x-1<log2x,
又f(log2x-1)>f(log2x),
∴f(x)是减函数,
有图象可知:3≤log2x-1<log2x≤4,或log2x-1<log2x≤-4,-2≤log2x-1<log2x≤0,
解得:x=16,或0<x≤
,或
≤x≤1
| 1 |
| 2 |
因为f(x)是r上的偶函数,
所以f(-1)=f(1)=
| 1 |
| 2 |
又C(4,0)D(5,1),结合图形可求得:
当x≥4时,f(x)=x-4,
故f(6)=6-4=2
(2)∵log2x-1<log2x,
又f(log2x-1)>f(log2x),
∴f(x)是减函数,
有图象可知:3≤log2x-1<log2x≤4,或log2x-1<log2x≤-4,-2≤log2x-1<log2x≤0,
解得:x=16,或0<x≤
| 1 |
| 16 |
| 1 |
| 2 |
点评:本题主要考查偶函数的性质和单调性,属于基础题.

练习册系列答案
相关题目
函数y=sin(2x-
)在区间[
,
]上的值域是( )
| π |
| 6 |
| π |
| 12 |
| π |
| 2 |
A、[-
| ||
B、[
| ||
| C、[0,1] | ||
D、[0,
|
数列{
}的前n项和为Sn,则S99=( )
| 1 |
| n(n+1) |
A、
| ||
B、
| ||
C、
| ||
D、
|
cos(-
π)的值是( )
| 43 |
| 6 |
A、
| ||||
B、
| ||||
C、-
| ||||
D、-
|
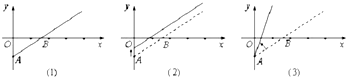 如图(1)是反应某公共汽车线路收支差额(即营运所得票价收入与付出成本的差)y与乘客两x之间关系的图象.由于目前该条公交线亏损,公司有关人员提出了两种调整的建议,如图(2)(3)的实线(虚线为原参考线)所示.给出下列说法:
如图(1)是反应某公共汽车线路收支差额(即营运所得票价收入与付出成本的差)y与乘客两x之间关系的图象.由于目前该条公交线亏损,公司有关人员提出了两种调整的建议,如图(2)(3)的实线(虚线为原参考线)所示.给出下列说法: