题目内容
1.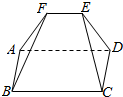 如图,在五面体ABCDEF中,四边形ABCD为正方形,BA⊥平面ADEF,DE⊥AF,AF=1,AD=2$\sqrt{2}$.
如图,在五面体ABCDEF中,四边形ABCD为正方形,BA⊥平面ADEF,DE⊥AF,AF=1,AD=2$\sqrt{2}$.(1)求异面直线BF与CD所成角的正弦值;
(2)证明:平面CDE⊥平面ABF.
分析 (1)由CD∥AB,得∠FBA就是异面直线BF与CD所成的角,由此能求出异面直线BF与CD所成角的正弦值.
(2)推导出DE⊥BA,DE⊥AF,由此能证明平面CDE⊥平面ABF.
解答 解:(1)∵四边形ABCD为正方形,∴CD∥AB,…(1分)
∴∠FBA就是异面直线BF与CD所成的角…(2分)
∵BA⊥平面ADEF,AF?平面ADEF,∴BA⊥AF,…(4分)
∵AF=1,$AB=AD=2\sqrt{2}$,
∴在直角△FBA中,$BF=\sqrt{A{B^2}+A{F^2}}=3$…(5分)
∴$sin∠FBA=\frac{AF}{BF}=\frac{1}{3}$,
∴异面直线BF与CD所成角的正弦值为$\frac{1}{3}$.…(6分)
证明:(2)∵BA⊥平面ADEF,DE?平面ADEF,∴DE⊥BA,…(7分)
由已知DE⊥AF…(8分)
∵BA,AF是平面ABF内的两条相交直线,…(9分)
∴DE⊥平面ABF,…(10分)
∵DE?平面CDE,∴平面CDE⊥平面ABF…(12分)
点评 本题考查异面直线所成角的正弦值的求法,考查面面垂直的证明,是中档题,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
11.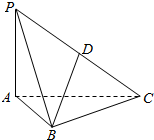 如图,PA⊥平面ABC,PA=$\sqrt{2}$,AB=1,BC=$\sqrt{3}$,AC=2,D是PC的中点.
如图,PA⊥平面ABC,PA=$\sqrt{2}$,AB=1,BC=$\sqrt{3}$,AC=2,D是PC的中点.
(1)求二面角B-PA-C的大小;
(2)求直线BD与平面ABC所成角的正切值.
 如图,PA⊥平面ABC,PA=$\sqrt{2}$,AB=1,BC=$\sqrt{3}$,AC=2,D是PC的中点.
如图,PA⊥平面ABC,PA=$\sqrt{2}$,AB=1,BC=$\sqrt{3}$,AC=2,D是PC的中点.(1)求二面角B-PA-C的大小;
(2)求直线BD与平面ABC所成角的正切值.
9.“a=$\frac{1}{2}$”是“直线l1:(a+2)x+(a-2)y=1与直线l2:(a-2)x+(3a-4)y=2相互垂直”的( )
| A. | 充分而不必要条件 | B. | 必要而不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
16.下面关于命题“p:所有抛物线的离心率为1”的说法正确的是( )
| A. | p是特称命题,¬p:存在一条抛物线的离心率不为1 | |
| B. | p是特称命题,¬p:存在一条抛物线的离心率为1 | |
| C. | p是全称命题,¬p:存在一条抛物线的离心率不为1 | |
| D. | p是全称命题,¬p:存在一条抛物线的离心率为1 |
10.已知A,B,C三点共线,且满足$\overrightarrow{CA}$=4sinx$\overrightarrow{OB}$+cosx$\overrightarrow{OC}$(O是不同于A,B,C的一点),则cos2x+sin2x=( )
| A. | $\frac{7}{17}$ | B. | $\frac{23}{17}$ | C. | -$\frac{23}{17}$ | D. | -$\frac{7}{17}$ |