题目内容
16.已知全集为R,集合A={0,1,2,3,4},B={x|x2-3x+2≤0},则A∩(∁RB)=( )| A. | {0,1,4} | B. | {1,2,4} | C. | {0,3,4} | D. | {1,2,3} |
分析 解一元二次不等式求得B,再根据补集的定义求得∁RB,再利用两个集合的交集的定义求得A∩∁RB.
解答 解:∵集合A={0,1,2,3,4},B={x|x2-3x+2≤0}={x|1≤x≤2},
∴∁RB={x|x<1,或x>2}
则A∩∁RB={0,3,4}
故选:C
点评 本题主要考查一元二次不等式的解法,集合的补集、两个集合的交集的定义和求法,属于基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
4.已知a>0,a≠1,x≠0,则${log_{a^2}}{x^2}$=( )
| A. | 2logax | B. | logax | C. | 2loga|x| | D. | loga|x| |
11.设P={x|x<1},下列关系式成立的是( )
| A. | ∅∈P | B. | 0∉P | C. | 0⊆P | D. | {0}⊆P |
8.执行如图所示的程序框图,则输出的S的值是( )
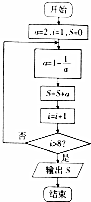

| A. | $\frac{9}{2}$ | B. | $\frac{5}{2}$ | C. | 3 | D. | $\frac{7}{2}$ |
5.已知tanα=-$\frac{3}{4}$,α∈(0,π),则cosα=( )
| A. | $\frac{4}{5}$ | B. | -$\frac{4}{5}$ | C. | ±$\frac{4}{5}$ | D. | $\frac{3}{5}$ |