题目内容
已知双曲线C:
-
=1(a>0,b>0),F1,F2为双曲线的左右焦点,若在双曲线的右焦点上存在一点P,使得|PF1|=3|PF2|,则双曲线的离心率的取值范围是 .
| x2 |
| a2 |
| y2 |
| b2 |
考点:双曲线的简单性质
专题:计算题,圆锥曲线的定义、性质与方程
分析:设P点的横坐标为x,根据|PF1|=3|PF2|,P在双曲线右支(x≥a),利用双曲线的第二定义,可得x关于e的表达式,进而根据x的范围确定e的范围.
解答:
解:设P点的横坐标为x
∵|PF1|=3|PF2|,P在双曲线右支(x≥a)
根据双曲线的第二定义,可得3e(x-
)=e(x+
)
∴ex=2a
∵x≥a,∴ex≥ea
∴2a≥ea,∴e≤2
∵e>1,∴1<e≤2
故答案为:1<e≤2.
∵|PF1|=3|PF2|,P在双曲线右支(x≥a)
根据双曲线的第二定义,可得3e(x-
| a2 |
| c |
| a2 |
| c |
∴ex=2a
∵x≥a,∴ex≥ea
∴2a≥ea,∴e≤2
∵e>1,∴1<e≤2
故答案为:1<e≤2.
点评:本题主要考查了双曲线的简单性质,考查了双曲线的第二定义的灵活运用,属于基础题.

练习册系列答案
 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案 初中暑期衔接系列答案
初中暑期衔接系列答案
相关题目
直线y=kx+b过原点的条件是( )
| A、k=0 |
| B、b=0 |
| C、k=0且b=0 |
| D、k≠0且b=0 |
下列现象是不可能现象的是( )
| A、导电通电时发热 |
| B、不共线的三点确定一个平面 |
| C、没有水分种子发芽 |
| D、某人买彩票连续两周都中奖 |
在△ABC中,三内角正弦之比sinA:sinB:sinC=2:3:
,则角C等于( )
| 7 |
| A、30° | B、45° |
| C、60° | D、120° |
 设
设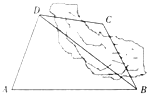 如图,为了计算某湖岸边两景点B与C的距离,由于地形的限制,需要岸上A和D两个测量点,现测得AD⊥CD,AD=10km,AB=14km,∠BDA=60°,∠BCD=135°,则两景点B与C之间的距离为(假设A,B,C,D在同一平面内)( )
如图,为了计算某湖岸边两景点B与C的距离,由于地形的限制,需要岸上A和D两个测量点,现测得AD⊥CD,AD=10km,AB=14km,∠BDA=60°,∠BCD=135°,则两景点B与C之间的距离为(假设A,B,C,D在同一平面内)( )