题目内容
已知△ABC,AC=BC=1,AB=
,又已知S是△ABC所在平面外一点,SA=SB=2,SC=
,点P是SC的中点,求点P到平面ABC的距离.
| 2 |
| 5 |
考点:点、线、面间的距离计算
专题:空间位置关系与距离
分析:作SD⊥AB,交AB于点D,连接CD,因为SA=SB,所以D是AB的中点.因为AC=BC,所以CD⊥AB.由勾股定理知△SCD为直角三角形.SD即为S到ABC的距离,由此能求出P到ABC的距离.
解答:
解:∵△ABC,AC=BC=1,AB=
,
又已知S是△ABC所在平面外一点,SA=SB=2,SC=
,
∴△ACB是等腰直角三角形,∠ACB=90°,
∠SAC=∠SBC=90°,
作SD⊥AB,交AB于点D,连接CD,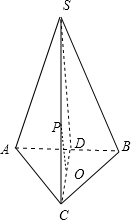
因为SA=SB,所以D是AB的中点.
因为AC=BC,所以CD⊥AB.
△SCD中,SC=
,
SD=
=
,
CD=
AB=
,
由勾股定理知△SCD为直角三角形.
SD即为S到ABC的距离,
P到ABC的距离为
=
.
| 2 |
又已知S是△ABC所在平面外一点,SA=SB=2,SC=
| 5 |
∴△ACB是等腰直角三角形,∠ACB=90°,
∠SAC=∠SBC=90°,
作SD⊥AB,交AB于点D,连接CD,

因为SA=SB,所以D是AB的中点.
因为AC=BC,所以CD⊥AB.
△SCD中,SC=
| 5 |
SD=
(
|
| 3 |
| 2 |
| 2 |
CD=
| 1 |
| 2 |
| ||
| 2 |
由勾股定理知△SCD为直角三角形.
SD即为S到ABC的距离,
P到ABC的距离为
| SD |
| 2 |
3
| ||
| 4 |
点评:本题考查点到平面的距离的求法,是中档题,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
相关题目
直线y=kx+b过原点的条件是( )
| A、k=0 |
| B、b=0 |
| C、k=0且b=0 |
| D、k≠0且b=0 |
直线3x-2y-4=0的截距方程是( )
A、
| ||||||||
B、
| ||||||||
C、
| ||||||||
D、
|
在△ABC中,已知ccosB=bcosC,则此三角形的形状为( )
| A、直角三角形 |
| B、等腰三角形 |
| C、等腰或直角三角形 |
| D、等腰直角三角形 |
 设
设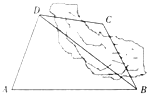 如图,为了计算某湖岸边两景点B与C的距离,由于地形的限制,需要岸上A和D两个测量点,现测得AD⊥CD,AD=10km,AB=14km,∠BDA=60°,∠BCD=135°,则两景点B与C之间的距离为(假设A,B,C,D在同一平面内)( )
如图,为了计算某湖岸边两景点B与C的距离,由于地形的限制,需要岸上A和D两个测量点,现测得AD⊥CD,AD=10km,AB=14km,∠BDA=60°,∠BCD=135°,则两景点B与C之间的距离为(假设A,B,C,D在同一平面内)( )