题目内容
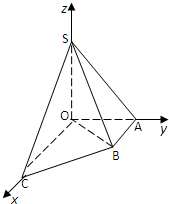 如图直角梯形OABC中,∠COA=∠OAB=90°,OC=2,OA=AB=1,SO⊥平面OABC,SO=1,分别以OC,OA,OS为x轴、y轴、z轴建立直角坐标系O-xyz.
如图直角梯形OABC中,∠COA=∠OAB=90°,OC=2,OA=AB=1,SO⊥平面OABC,SO=1,分别以OC,OA,OS为x轴、y轴、z轴建立直角坐标系O-xyz.(Ⅰ)求
| SC |
| OB |
(Ⅱ)求OC与平面SBC夹角的正弦值;
(Ⅲ)求二面角S-BC-O.
考点:用空间向量求平面间的夹角,异面直线及其所成的角,与二面角有关的立体几何综合题
专题:综合题,空间角,空间向量及应用
分析:(Ⅰ)根据已知,求出各顶点的坐标,进而求出向量
与
的坐标,代入向量夹角公式,即可得到结论.
(Ⅱ)求出平面SBC的法向量,
=(2,0,0),利用向量的夹角公式,即可求OC与平面SBC夹角的正弦值;
(Ⅲ)求出平面OABC的法向量,平面SBC的法向量,利用向量的夹角公式,即可求二面角S-BC-O.
| SC |
| OB |
(Ⅱ)求出平面SBC的法向量,
| OC |
(Ⅲ)求出平面OABC的法向量,平面SBC的法向量,利用向量的夹角公式,即可求二面角S-BC-O.
解答:
 解:(Ⅰ)如图所示:C(2,0,0),S(0,0,1),O(0,0,0),B(1,1,0).
解:(Ⅰ)如图所示:C(2,0,0),S(0,0,1),O(0,0,0),B(1,1,0).
∴
=(2,0,-1),
=(1,1,0),
∴cos<
,
>=
=
.
∴
与
夹角的余弦值为
. …(3分)
(Ⅱ)设平面SBC的法向量
=(1,p,q),
∵
=(2,0,-1),
=(-1,1,0),
∴
,∴
,
∴
=(1,1,2),…(6分)
又∵
=(2,0,0),
∴cos<
,
>=
=
=
∴OC与平面SBC夹角的正弦值为
;…(8分)
(Ⅲ)∵SO⊥平面OABC,∴
=(0,0,1)为平面OABC的法向量.
又∵平面SBC的法向量
=(1,1,2),
∴cos<
,
>=
=
=
.
∴二面角S-BC-O的余弦值为
.…(12分)
 解:(Ⅰ)如图所示:C(2,0,0),S(0,0,1),O(0,0,0),B(1,1,0).
解:(Ⅰ)如图所示:C(2,0,0),S(0,0,1),O(0,0,0),B(1,1,0).∴
| SC |
| OB |
∴cos<
| SC |
| OB |
| 2 | ||||
|
| ||
| 5 |
∴
| SC |
| OB |
| ||
| 5 |
(Ⅱ)设平面SBC的法向量
| n |
∵
| SC |
| CB |
∴
|
|
∴
| n |
又∵
| OC |
∴cos<
| n |
| OC |
| ||||
|
|
| 2 | ||
|
| ||
| 6 |
∴OC与平面SBC夹角的正弦值为
| ||
| 6 |
(Ⅲ)∵SO⊥平面OABC,∴
| OS |
又∵平面SBC的法向量
| n |
∴cos<
| n |
| OS |
| ||||
|
|
| 2 | ||
|
| ||
| 3 |
∴二面角S-BC-O的余弦值为
| ||
| 3 |
点评:本题考查空间角的计算,考查向量法的运用,正确求出平面的法向量是关键.

练习册系列答案
 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案
相关题目
已知向量
=(1,-2),
=(x,4),且
∥
,则|
-
|=( )
| a |
| b |
| a |
| b |
| a |
| b |
A、5
| ||
B、3
| ||
C、2
| ||
D、2
|
已知在一个120°的二面角的棱上有两个点A、B,AC、BD分别是在这个二面角的两个半平面内且垂直于AB的线段,又AB=4cm,AC=6cm,BD=8cm,则CD的长为( )
A、2
| ||
B、
| ||
C、2
| ||
D、4
|
 已知△ABC的两顶点坐标A(-1,0),B(1,0),圆E是△ABC的内切圆,在边AC,BC,AB上的切点分别为P,Q,R,|CP|=1(从圆外一点到圆的两条切线段长相等),动点C的轨迹为曲线M.
已知△ABC的两顶点坐标A(-1,0),B(1,0),圆E是△ABC的内切圆,在边AC,BC,AB上的切点分别为P,Q,R,|CP|=1(从圆外一点到圆的两条切线段长相等),动点C的轨迹为曲线M. 在如图所示的空间几何体中,平面ACD⊥平面ABC,△ACD与△ACB是边长为2的等边三角形,BE=2,BE和平面ABC所成的角为60°,且点E在平面ABC上的射影落在∠ABC的平分线上.
在如图所示的空间几何体中,平面ACD⊥平面ABC,△ACD与△ACB是边长为2的等边三角形,BE=2,BE和平面ABC所成的角为60°,且点E在平面ABC上的射影落在∠ABC的平分线上. 选修4-1几何证明选讲
选修4-1几何证明选讲