题目内容
己知某几何体的三视图如图所示，则该几何体的体积是（ ）
A、
| ||||
B、
| ||||
C、2
| ||||
D、2
|
考点：由三视图求面积、体积
专题：计算题,空间位置关系与距离
分析：根据三视图判断几何体是三棱柱与半圆柱的组合体，且三棱柱的底面是边长为2的正三角形，高为2；半圆柱的底面半径为1，高为2，把数据代入棱柱与半圆柱的体积公式计算．
解答：
解：由三视图知几何体是三棱柱与半圆柱的组合体，且三棱柱的底面是边长为2的正三角形，高为2；
半圆柱的底面半径为1，高为2，
∴几何体的体积V=
×2×
×2+
×π×12×2=2
+π．
故选D．
半圆柱的底面半径为1，高为2，
∴几何体的体积V=
| 1 |
| 2 |
| 3 |
| 1 |
| 2 |
| 3 |
故选D．
点评：本题考查了由三视图求几何体的体积，判断几何体的形状及数据所对应的几何量是解答此类问题的关键．
练习册系列答案
相关题目
已知向量
=(1，-2)，
=(x，4)，且
∥
，则|
-
|=（ ）
| a |
| b |
| a |
| b |
| a |
| b |
A、5
| ||
B、3
| ||
C、2
| ||
D、2
|
定义域为R的函数f（x）满足f（x+2）=2f（x），当x∈[0，2]时，f(x)=
，若x∈[-2，0]时，f(x)≥
-
恒成立，则实数t的取值范围是（ ）
|
| t |
| 2 |
| 1 |
| t |
| A、[-2，0）∪（0，1） |
| B、[-2，0）∪[1，+∞） |
| C、[-2，1] |
| D、（-∞，-2]∪（0，1] |
阅读如图所示的程序框图，则该算法的功能是（ ）
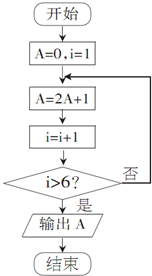
| A、计算数列{2n-1}前5项的和 |
| B、计算数列{2n-1}前6项的和 |
| C、计算数列{2n-1}前5项的和 |
| D、计算数列{2n-1}前6项的和 |
已知在一个120°的二面角的棱上有两个点A、B，AC、BD分别是在这个二面角的两个半平面内且垂直于AB的线段，又AB=4cm，AC=6cm，BD=8cm，则CD的长为（ ）
A、2
| ||
B、
| ||
C、2
| ||
D、4
|
选修4-1几何证明选讲