题目内容
11.已知两条不同直线m,n,两个不同平面α,β,给出下列命题:①若n∥α,则n平行于α内的所有直线;
②若m⊥α,n∥α,则m⊥n;
③若m?α,n?β且n⊥m,则α⊥β;
④若n?β,n⊥α,则α⊥β
其中正确命题的序号是( )
| A. | ①④ | B. | ②④ | C. | ②③ | D. | ③④ |
分析 ①,若n∥α,则n与α内的直线平行或异面;
②,根据线面平行的性质判定;
③,结合面面垂直的判定定理进行判断;
④,根据面面垂直的判定
解答 解:对于①,若n∥α,则n与α内的直线平行或异面,故错;
对于②,若m⊥α,n∥α,根据线面平行的性质知,必有lm⊥n,故正确;
对于③,若m?α,n?β且n⊥m,结合面面垂直的判定定理,可得α与β不一定垂直,故错;
对于④,若n?β,n⊥α,根据面面垂直的判定,可得α⊥β,故正确;
故选:B.
点评 题考查空间线线、线面、面面位置关系,涉及到了面面平行的判断,面面垂直的判断,线面垂直的定义,属于基础知识考查题.

练习册系列答案
 星级口算天天练系列答案
星级口算天天练系列答案
相关题目
16.若函数$f(x)=\sqrt{1-{x^2}}$的图象上某一点处的切线过点(2,1),则切线的斜率为( )
| A. | 0 | B. | 0或$\frac{4}{3}$ | C. | $\frac{4}{5}$ | D. | $\frac{4}{3}$ |
20.已知集合A={y|y=2cos2x-1},B={x|y=$\sqrt{2x-{x}^{2}}$},则A∪B=( )
| A. | {x|-1≤x≤0} | B. | {x|0≤x<1} | C. | {x|-1<x<2} | D. | {x|-1≤x≤2} |
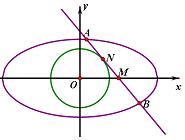 已知椭圆$C:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$的右焦点$(\sqrt{3},0)$,且经过点$(-1,\frac{{\sqrt{3}}}{2})$,点M是x轴上的一点,过点M的直线l与椭圆C交于A,B两点(点A在x轴的上方)
已知椭圆$C:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$的右焦点$(\sqrt{3},0)$,且经过点$(-1,\frac{{\sqrt{3}}}{2})$,点M是x轴上的一点,过点M的直线l与椭圆C交于A,B两点(点A在x轴的上方)