题目内容
18.如图甲,边长为2的正方形ABCD中,点E,F分别是边AB和BC上的点.(1)若点E是AB的中点,点F是BC的中点时,将△AED,△DCF分别沿DE,DF折起,使A,C两点重合于点A(如图乙),求证:A1D⊥EF;
(2)当BE=BF=$\frac{1}{4}$BC时,求三棱锥A1-EFD的体积.
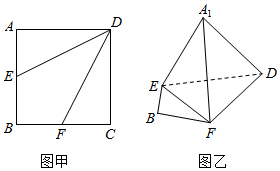
分析 (1)由A1D⊥A1F,A1D⊥A1E可得A1D⊥平面A1EF,故A1D⊥EF;
(2)在△A1EF中,使用余弦定理求出cos∠EA1F,得出sin∠EA1F,则V${\;}_{{A}_{1}-EFD}$=V${\;}_{D-{A}_{1}EF}$.
解答 解:(1)∵四边形ABCD是正方形,
∴A1D⊥A1F,A1D⊥A1E,
又∵A1E∩A1F=A1,A1E?平面A1EF,A1F?平面A1EF.
∴A1D⊥平面A1EF.又∵EF?平面A1EF,
∴A1D⊥EF.
(2)由四边形ABCD为边长为2的正方形,BE=BF=$\frac{1}{4}$BC=$\frac{1}{2}$.
∴${A_1}D=2,{A_1}E={A_1}F=\frac{3}{2},EF=\frac{{\sqrt{2}}}{2}$,
在△A1EF中,由余弦定理得:$cos∠E{A_1}F=\frac{{{{({\frac{3}{2}})}^2}+{{({\frac{3}{2}})}^2}-{{({\frac{{\sqrt{2}}}{2}})}^2}}}{{2×\frac{3}{2}×\frac{3}{2}}}=\frac{8}{9}$,
∴$sin∠E{A_1}F=\frac{{\sqrt{17}}}{9}$
∴${S_{△E{A_1}F}}=\frac{1}{2}{A_1}E•{A_1}F•sin∠E{A_1}F=\frac{{\sqrt{17}}}{8}$
∴三棱锥A1-EFD的体积$V=\frac{1}{3}×\frac{{\sqrt{17}}}{8}×2=\frac{{\sqrt{17}}}{12}$.
点评 本题考查了线面垂直的判定与性质,棱锥的体积计算,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
8.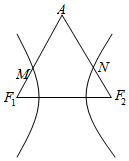 (普通中学做)如图,已知F1、F2为双曲线的两焦点,等边三角形AF1F2两边的中点M、N在双曲线上,则该双曲线的离心率为( )
(普通中学做)如图,已知F1、F2为双曲线的两焦点,等边三角形AF1F2两边的中点M、N在双曲线上,则该双曲线的离心率为( )
 (普通中学做)如图,已知F1、F2为双曲线的两焦点,等边三角形AF1F2两边的中点M、N在双曲线上,则该双曲线的离心率为( )
(普通中学做)如图,已知F1、F2为双曲线的两焦点,等边三角形AF1F2两边的中点M、N在双曲线上,则该双曲线的离心率为( )| A. | $\sqrt{3}$+1 | B. | $\sqrt{2}$+1 | C. | $\sqrt{5}$+1 | D. | $\sqrt{5}$-1 |
6.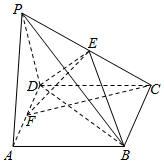 如图,在四棱锥P-ABCD中,底面ABCD是正方形,侧面PAD是边长为2的正三角形,PD⊥CD,E,F分别为PC,AD的中点.
如图,在四棱锥P-ABCD中,底面ABCD是正方形,侧面PAD是边长为2的正三角形,PD⊥CD,E,F分别为PC,AD的中点.
(1)求证:平面CEF⊥平面ABCD;
(2)求三棱锥P-BDE的体积.
 如图,在四棱锥P-ABCD中,底面ABCD是正方形,侧面PAD是边长为2的正三角形,PD⊥CD,E,F分别为PC,AD的中点.
如图,在四棱锥P-ABCD中,底面ABCD是正方形,侧面PAD是边长为2的正三角形,PD⊥CD,E,F分别为PC,AD的中点.(1)求证:平面CEF⊥平面ABCD;
(2)求三棱锥P-BDE的体积.
7.下列四个式子中是恒等式的是( )
| A. | sin(α+β)=sinα+sinβ | B. | cos(α+β)=cosαcosβ+sinβsinβ | ||
| C. | tan(α+β)=$\frac{tanα-tanβ}{1-tanαtanβ}$ | D. | sin(α+β)sin(α-β)=sin2α-sin2β |
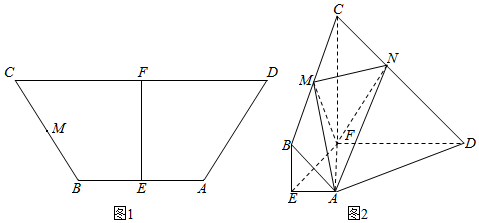
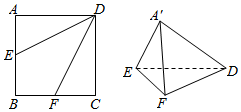 如图,E、F是正方形ABCD的边AB、BC的中点,将△ADE、△CDF、△BEF分别沿DE、DF、EF折起,使A、B、C三点重合于点A′.
如图,E、F是正方形ABCD的边AB、BC的中点,将△ADE、△CDF、△BEF分别沿DE、DF、EF折起,使A、B、C三点重合于点A′.