题目内容
6.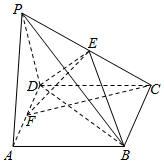 如图,在四棱锥P-ABCD中,底面ABCD是正方形,侧面PAD是边长为2的正三角形,PD⊥CD,E,F分别为PC,AD的中点.
如图,在四棱锥P-ABCD中,底面ABCD是正方形,侧面PAD是边长为2的正三角形,PD⊥CD,E,F分别为PC,AD的中点.(1)求证:平面CEF⊥平面ABCD;
(2)求三棱锥P-BDE的体积.
分析 (1)连结PF,由CD⊥AD,CD⊥PD得CD⊥平面PAD,故CD⊥PF,又PF⊥AD,故PF⊥平面ABCD,于是平面CEF⊥平面ABCD;
(2)由E是PC的中点得VP-BDE=$\frac{1}{2}$VP-BDC.
解答  解:(1)连结PF,
解:(1)连结PF,
∵△PAD是正三角形,∴PF⊥AD.
∵AD⊥CD,PD⊥CD,PD?平面PAD,AD?平面PAD,AD∩PD=D,
∴CD⊥平面PAD,∵PF?平面PAD,
∴CD⊥PF.
又∵AD?平面ABCD,CD?平面ABCD,AD∩CD=D,
∴PF⊥平面ABCD,∵PF?平面CEF,
∴平面CEF⊥平面ABCD.
(2)∵△PAD是边长为2的正三角形,四边形ABCD是边长为2的正方形,
∴PF=$\sqrt{3}$,BC=CD=2,
∴VP-BCD=$\frac{1}{3}{S}_{△BCD}•PF$=$\frac{1}{3}×\frac{1}{2}×{2}^{2}×\sqrt{3}$=$\frac{2\sqrt{3}}{3}$.
∵E是PC的中点,
∴VP-BDE=$\frac{1}{2}$VP-BDC=$\frac{\sqrt{3}}{3}$.
点评 本题考查了线面垂直,面面垂直的判定,棱锥的体积计算,属于中档题.

练习册系列答案
 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案
相关题目
14. 如图网格纸上小正方形的边长为l,粗实线画出的是某几何体的三视图,则这个几何体的体积为( )
如图网格纸上小正方形的边长为l,粗实线画出的是某几何体的三视图,则这个几何体的体积为( )
 如图网格纸上小正方形的边长为l,粗实线画出的是某几何体的三视图,则这个几何体的体积为( )
如图网格纸上小正方形的边长为l,粗实线画出的是某几何体的三视图,则这个几何体的体积为( )| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
 如图,三棱柱ABC-A1B1C1中,AA1⊥平面ABC,BC⊥AC,BC=AC=2,AA1=3D为AC的中点
如图,三棱柱ABC-A1B1C1中,AA1⊥平面ABC,BC⊥AC,BC=AC=2,AA1=3D为AC的中点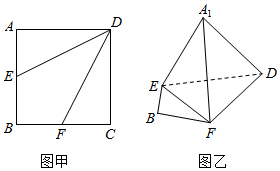
 如图,在四面体ABCD中,CD=CB,AD⊥BD,点E,F分别是AB,BD的中点.
如图,在四面体ABCD中,CD=CB,AD⊥BD,点E,F分别是AB,BD的中点.