题目内容
8．
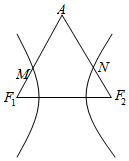（普通中学做）如图，已知F1、F2为双曲线的两焦点，等边三角形AF1F2两边的中点M、N在双曲线上，则该双曲线的离心率为（ ）| A． | $\sqrt{3}$+1 | B． | $\sqrt{2}$+1 | C． | $\sqrt{5}$+1 | D． | $\sqrt{5}$-1 |
分析 设|F1F2|=2c，由题意可得|MF1|=c，再由等边三角形的高可得|MF2|=$\sqrt{3}$c，运用双曲线的定义和离心率公式，计算即可得到所求值．
解答 解：设|F1F2|=2c，由题意可得|MF1|=c，
由MF2为等边三角形AF1F2的高，可得：
|MF2|=$\sqrt{3}$c，
由双曲线的定义可得|MF2|-|MF1|=$\sqrt{3}$c-c，
由e=$\frac{2c}{2a}$=$\frac{2c}{\sqrt{3}c-c}$=1+$\sqrt{3}$，
故选：A．
点评 本题考查双曲线的离心率的求法，注意运用等边三角形的性质和双曲线的定义，考查运算能力，属于基础题．
练习册系列答案
相关题目
2．已知集合P={（x，y）|$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）}，Q={（x，y）|$\frac{x}{a}$+$\frac{y}{b}$＞m（a＞b＞0，m＞0）}，若?M∈P，M∉Q，则实数m的取值范围是（ ）
| A． | [$\sqrt{2}$，+∞） | B． | [2$\sqrt{2}$，+∞） | C． | [$\frac{\sqrt{6}}{6}$，+∞） | D． | （-∞，0] |
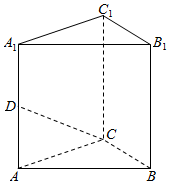如图，三棱柱ABC-A1B1C1中，侧棱AA1⊥底面ABC，AA1=AB=2，BC=1，$∠BAC=\frac{π}{6}$，D为棱AA1中点，证明异面直线B1C1与CD所成角为$\frac{π}{2}$，并求三棱柱ABC-A1B1C1的体积．
13．在空间直角坐标系中，点B是点A（1，2，3）在坐标平面xOy上的射影，O为坐标原点，则OB的长为（ ）
| A． | $\sqrt{10}$ | B． | $\sqrt{13}$ | C． | $\sqrt{14}$ | D． | $\sqrt{5}$ |
