题目内容
7.下列四个式子中是恒等式的是( )| A. | sin(α+β)=sinα+sinβ | B. | cos(α+β)=cosαcosβ+sinβsinβ | ||
| C. | tan(α+β)=$\frac{tanα-tanβ}{1-tanαtanβ}$ | D. | sin(α+β)sin(α-β)=sin2α-sin2β |
分析 对4个选项分别进行判断,即可得出结论.
解答 解:sin(α+β)=sinαcosβ+cosαsinβ,故A不正确;
cos(α+β)=cosαcosβ-sinβsinβ,故B不正确;
tan(α+β)=$\frac{tanα+tanβ}{1-tanαtanβ}$,故不正确;
sin(α+β)sin(α-β)=(sinαcosβ+cosαsinβ)(sinαcosβ-cosαsinβ)=sin2α-sin2β,正确.
故选:D.
点评 本题考查三角函数知识的运用,考查学生对公式的理解,考查学生的计算能力,正确理解公式是关键.

练习册系列答案
相关题目
2.曲线y=ex+1在点(0,2)处的切线与直线y=0和x=0围成的三角形面积为( )
| A. | $\frac{1}{2}$ | B. | $\frac{2}{3}$ | C. | 1 | D. | 2 |
19.已知f(x)=sin(x+$\frac{π}{6}$),若sinα=$\frac{3}{5}$(0<α<$\frac{π}{2}}$),则f(α+$\frac{π}{12}}$)=( )
| A. | $-\frac{{7\sqrt{2}}}{10}$ | B. | $-\frac{{\sqrt{2}}}{10}$ | C. | $\frac{{\sqrt{2}}}{10}$ | D. | $\frac{{7\sqrt{2}}}{10}$ |
17.若方程x2+$\frac{{y}^{2}}{a}$=1(a是常数),则下列结论正确的是( )
| A. | 任意实数a方程表示椭圆 | B. | 存在实数a方程表示椭圆 | ||
| C. | 任意实数a方程表示双曲线 | D. | 存在实数a方程表示抛物线 |
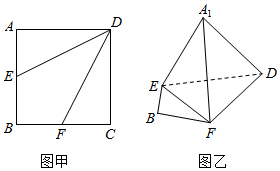
 如图,在四面体ABCD中,CD=CB,AD⊥BD,点E,F分别是AB,BD的中点.
如图,在四面体ABCD中,CD=CB,AD⊥BD,点E,F分别是AB,BD的中点.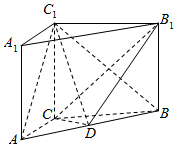 如图,在三棱柱ABC-A1B1C1中,CC1⊥平面ABC,AC=3,BC=4,AB=5,AA1=4,点D是AB的中点.
如图,在三棱柱ABC-A1B1C1中,CC1⊥平面ABC,AC=3,BC=4,AB=5,AA1=4,点D是AB的中点.