题目内容
13.等比数列{an}中,若a3,a11是方程2x2-23x+56=0的两个根,则a7=$2\sqrt{7}$.分析 由题意可得a3•a11=$\frac{56}{2}=28$,且得到数列{an}中的奇数项大于0,然后再由等比数列的性质求得a7.
解答 解:由a3,a11是方程2x2-23x+56=0的两个根,得
a3+a11=$\frac{23}{2}$,a3•a11=$\frac{56}{2}=28$,则a3>0,
∵数列{an}是等比数列,
∴${{a}_{7}}^{2}={a}_{3}{a}_{11}=28$,
∴${a}_{7}=-2\sqrt{7}$,或${a}_{7}=2\sqrt{7}$,
由上面a3>0,又由等比数列的性质知,比数列中所有奇数项都是同号,
可知${a}_{7}=2\sqrt{7}$.
故答案为:$2\sqrt{7}$.
点评 本题考查等比数列的通项公式,考查了一元二次方程根与系数关系的应用,是基础题.

练习册系列答案
相关题目
8.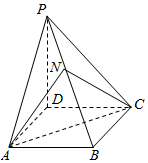 如图,四棱锥P-ABCD的底面ABCD为平行四边形,NB=2PN,则三棱锥N-PAC与四棱锥P-ABCD的体积比为( )
如图,四棱锥P-ABCD的底面ABCD为平行四边形,NB=2PN,则三棱锥N-PAC与四棱锥P-ABCD的体积比为( )
 如图,四棱锥P-ABCD的底面ABCD为平行四边形,NB=2PN,则三棱锥N-PAC与四棱锥P-ABCD的体积比为( )
如图,四棱锥P-ABCD的底面ABCD为平行四边形,NB=2PN,则三棱锥N-PAC与四棱锥P-ABCD的体积比为( )| A. | 1:2 | B. | 1:3 | C. | 1:6 | D. | 1:8 |
2.曲线y=ex+1在点(0,2)处的切线与直线y=0和x=0围成的三角形面积为( )
| A. | $\frac{1}{2}$ | B. | $\frac{2}{3}$ | C. | 1 | D. | 2 |
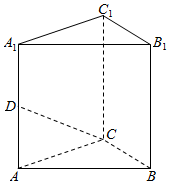 如图,三棱柱ABC-A1B1C1中,侧棱AA1⊥底面ABC,AA1=AB=2,BC=1,$∠BAC=\frac{π}{6}$,D为棱AA1中点,证明异面直线B1C1与CD所成角为$\frac{π}{2}$,并求三棱柱ABC-A1B1C1的体积.
如图,三棱柱ABC-A1B1C1中,侧棱AA1⊥底面ABC,AA1=AB=2,BC=1,$∠BAC=\frac{π}{6}$,D为棱AA1中点,证明异面直线B1C1与CD所成角为$\frac{π}{2}$,并求三棱柱ABC-A1B1C1的体积. 如图,三棱柱ABC-A1B1C1中,AA1⊥平面ABC,BC⊥AC,BC=AC=2,AA1=3D为AC的中点
如图,三棱柱ABC-A1B1C1中,AA1⊥平面ABC,BC⊥AC,BC=AC=2,AA1=3D为AC的中点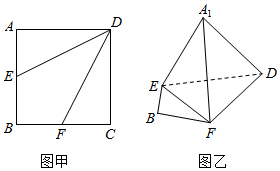
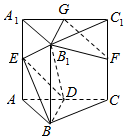 三棱柱ABC-A1B1C1中,侧棱AA1⊥平面ABC,各棱长均为2,D,E,F,G分别是棱AC,AA1,CC1,A1C1的中点.
三棱柱ABC-A1B1C1中,侧棱AA1⊥平面ABC,各棱长均为2,D,E,F,G分别是棱AC,AA1,CC1,A1C1的中点.