题目内容
10.设全集U={x∈R|x>0},函数f(x)=$\frac{1}{\sqrt{lnx-1}}$的定义域为A,则∁UA为( )| A. | (0,e] | B. | (0,e) | C. | (e,+∞) | D. | [e,+∞) |
分析 先求出集合A,由此能求出CUA.
解答 解:∵全集U={x∈R|x>0},
函数f(x)=$\frac{1}{\sqrt{lnx-1}}$的定义域为A,
∴A={x|x>e},
∴∁UA={x|0<x≤e}=(0,e].
故选:A.
点评 本题考查补集的求法,是基础题,解题时要认真审题,注意补集定义的合理运用.

练习册系列答案
 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案
相关题目
20.已知点M的极坐标为(6,$\frac{11π}{6}$),则点M关于y轴对称的点的直角坐标为( )
| A. | (-3$\sqrt{3}$,-3) | B. | (3$\sqrt{3}$,-3) | C. | (-3$\sqrt{3}$,3) | D. | (3$\sqrt{3}$,3) |
19.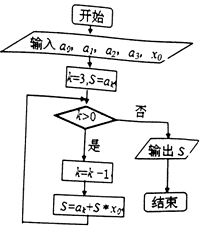 秦九韶是我国南宋时代的数学家,其代表作《数书九章》是我国13世纪数学成就的代表之一;如图是秦九韶算法的一个程序框图,则输出的S为( )
秦九韶是我国南宋时代的数学家,其代表作《数书九章》是我国13世纪数学成就的代表之一;如图是秦九韶算法的一个程序框图,则输出的S为( )
 秦九韶是我国南宋时代的数学家,其代表作《数书九章》是我国13世纪数学成就的代表之一;如图是秦九韶算法的一个程序框图,则输出的S为( )
秦九韶是我国南宋时代的数学家,其代表作《数书九章》是我国13世纪数学成就的代表之一;如图是秦九韶算法的一个程序框图,则输出的S为( )| A. | a1+x0(a3+x0(a0+a2x0))的值 | B. | a3+x0(a2+x0(a1+a0x0))的值 | ||
| C. | a0+x0(a1+x0(a2+a3x0))的值 | D. | a2+x0(a0+x0(a3+a1x0))的值 |
8.已知函数f(x)=$\frac{4}{3}$x3-2kx2-x+1有两个不同的极值点x1,x2(x1<1<x2),若g(x)=$\frac{2x-k}{{x}^{2}+1}$,且x∈[1,x2]时,g(x)≥$\frac{k}{2}$恒成立,则实数k的取值范围是( )
| A. | ($\frac{3}{4}$,+∞) | B. | [1,+∞) | C. | ($\frac{3}{4}$,1] | D. | {1} |
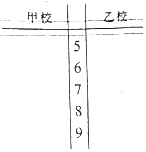 某市对创“市级示范性学校”的甲、乙两所学校进行复查验收,对办学的社会满意度一项评价随机访问了20位市民,这20位市民对这两所学校的评分(评分越高表明市民的评价越好)的数据如下:
某市对创“市级示范性学校”的甲、乙两所学校进行复查验收,对办学的社会满意度一项评价随机访问了20位市民,这20位市民对这两所学校的评分(评分越高表明市民的评价越好)的数据如下: