题目内容
9．已知a1=1，an-an-1=2（n≥2，n∈N*），则{an}的前n项和为n2．分析 利用等差数列的定义、前n项和公式即可得出．
解答 解：由a1=1，an-an-1=2（n≥2，n∈N*），数列{an}是等差数列，首项为1，公差为2，
∴前n项和Sn=n+$\frac{n（n-1）}{2}×2$=n2．
故答案为：n2．
点评 本题考查了等差数列的性质、等差数列的定义、前n项和公式，考查了推理能力与计算能力，属于中档题．
练习册系列答案
相关题目
20．已知sin（α+π）=$\frac{1}{2}$，且$α∈（-\frac{π}{2}，0）$，则tanα的值为（ ）
| A． | $-\frac{{\sqrt{3}}}{3}$ | B． | $\sqrt{3}$ | C． | $-\frac{1}{2}$ | D． | $\frac{{\sqrt{3}}}{3}$ |
14．函数y=cos（2x-$\frac{π}{2}$）是（ ）
| A． | 最小正周期为2π的偶函数 | B． | 最小正周期为π的偶函数 | ||
| C． | 最小正周期为2π的奇函数 | D． | 最小正周期为π的奇函数 |
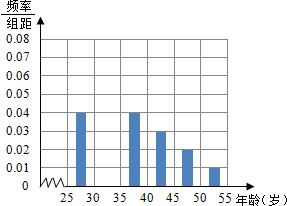某班同学参加社会实践活动，本市25～55岁年龄段的人群进行某项随机调查，得到各年龄段被调查人数的频率分布直方图如下（部分缺损）