��Ŀ����
1��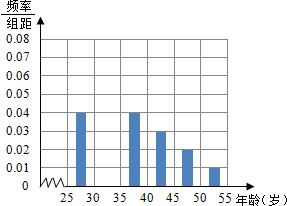 ij��ͬѧ�μ����ʵ���������25��55������ε���Ⱥ����ij��������飬�õ�������α�����������Ƶ�ʷֲ�ֱ��ͼ���£�����ȱ��
ij��ͬѧ�μ����ʵ���������25��55������ε���Ⱥ����ij��������飬�õ�������α�����������Ƶ�ʷֲ�ֱ��ͼ���£�����ȱ����1����ȫƵ��ֱ��ͼ����д��������̣���
��2���ִ�[40��55���������в��÷ֲ����������ȡ6�˷ֳ�A��B����С�飨ÿ��3�ˣ��μӻ�����������A����������[40��50���������Ϊ�Σ�����������εķֲ��к���ѧ����E�Σ�
��3���ִ�[40��55��������������в��÷ֲ����������ȡ6�˷ֳ�A��B����С�飨ÿ��3�ˣ��μӻ�����������A����3������������ͬ����εĸ��ʣ�
���� ��1��������ڶ����Ƶ�ʣ�������ߣ��ɴ�������Ƶ��ֱ��ͼ��
��2��[40��45���飬[45��50�����[50��55�����������Ϊ3��2��1���Ӷ������г���������ֱ�Ϊ3��2��1����=0��1��2��3���ֱ������Ӧ�ĸ��ʣ��ɴ�������εķֲ��к�E�Σ�
��3��[40��45���飬[45��50�����[50��55�����г���������ֱ�Ϊ3��2��1���ɴ������A����3������������ͬ����εĸ��ʣ�
��� �⣺��1���ߵڶ����Ƶ��Ϊ1-��0.04+0.04+0.03+0.02+0.01����5=0.3��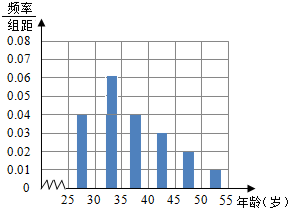
���Ϊ0.3��5=0.06��
����Ƶ��ֱ��ͼ������ͼ��
��2����[40��45���飬[45��50�����[50��55�����������Ϊ0.03��0.02��0.01=3��2��1��
�������г���������ֱ�Ϊ3��2��1��
��=0��1��2��3��
P����=0��=$\frac{{C}_{3}^{0}}{{C}_{6}^{3}}$=$\frac{1}{20}$��P����=1��=$\frac{{C}_{3}^{1}{C}_{3}^{2}}{{C}_{6}^{3}}$=$\frac{9}{20}$��
P����=2��=$\frac{{C}_{3}^{2}{C}_{3}^{1}}{{C}_{6}^{3}}$=$\frac{9}{20}$��P����=3��=$\frac{{C}_{3}^{3}}{{C}_{6}^{3}}$=$\frac{1}{20}$��
��εķֲ���Ϊ��
| �� | 0 | 1 | 2 | 3 |
| P | $\frac{1}{20}$ | $\frac{9}{20}$ | $\frac{9}{20}$ | $\frac{1}{20}$ |
��3���ɣ�2��֪��[40��45���飬[45��50�����[50��55�����������Ϊ0.03��0.02��0.01=3��2��1��
�������г���������ֱ�Ϊ3��2��1��
A����3������������ͬ����εĸ��ʣ�p=$\frac{{C}_{3}^{1}{C}_{2}^{1}{C}_{1}^{1}}{{C}_{6}^{3}}$=$\frac{3}{10}$��
���� ���⿼��Ƶ�ʷֲ�ֱ��ͼ��������������ɢ����������ķֲ��С���ѧ��������������ʵ���������߿��ж��DZؿ�����֮һ��

| A�� | 1�� | B�� | 2�� | C�� | 3�� | D�� | 4�� |
| A�� | ���⡰p��q��Ϊ�����⣬�����⡰p�������⡰q����Ϊ������ | |
| B�� | ��am2��bm2���ǡ�a��b���ı�Ҫ��������� | |
| C�� | ����p������x0��R��ʹ��x02+x0+1��0����Vp������x∉R������x2+x+1��0 | |
| D�� | ���⡰��x2��1����-1��x��1���������������x��1��x��-1����x2��1 |
| A�� | $\frac{1}{{2}^{x}}$��$\frac{1}{{3}^{x}}$ | B�� | $\frac{1}{{x}^{2}-x+1}$��$\frac{1}{{x}^{2}+x+1}$ | ||
| C�� | $\frac{1}{{x}^{2}+1}$��$\frac{1}{{x}^{2}+2}$ | D�� | $\frac{1}{2|x|}$��$\frac{1}{{x}^{2}+1}$ |
| A�� | $\frac{13}{5}$ | B�� | 3 | C�� | $\frac{5}{2}$ | D�� | 6 |