题目内容
19.设f'(x)是函数f(x)的导数,f''(x)是函数f'(x)的导数,若方程f''(x)=0有实数解x0,则称点(x0,f(x0))为函数f(x)的拐点.某同学经过探究发现:任何一个三次函数f(x)=ax3+bx2+cx+d(a≠0)都有拐点,任何一个三次函数都有对称中心,且拐点就是对称中心,设函数g(x)=x3-3x2+4x+2,利用上述探究结果
计算:$g(\frac{1}{10})+g(\frac{2}{10})+g(\frac{3}{10})+…+g(\frac{19}{10})$=76.
分析 根据函数g(x)的解析式求出g′(x)和g″(x),令g″(x)=0,求得x的值,由此求得三次函数g(x)的对称中心.由于函数的对称中心为(1,4),可知g(x)+f(2-x)=8,由此能够求出所给的式子的值.
解答 解:由g(x)=x3-3x2+4x+2,
得:g′(x)=3x2-6x+4,g″(x)=6x-6,
令g″(x)=0,解得:x=1,
∴函数g(x)的对称中心是(1,4),
∴g(2-x)+g(x)=8,
故设$g(\frac{1}{10})+g(\frac{2}{10})+g(\frac{3}{10})+…+g(\frac{19}{10})$=m,
则g($\frac{19}{10}$)+g($\frac{18}{10}$)+g($\frac{17}{10}$)+…+g($\frac{1}{10}$)=m,
两式相加得:8×19=2m,解得:m=76,
故答案为:76.
点评 本小题主要考查函数与导数等知识,考查化归与转化的数学思想方法,考查化简计算能力,求函数的值以及函数的对称性的应用,属于中档题.

练习册系列答案
 科学实验活动册系列答案
科学实验活动册系列答案
相关题目
10.某人从甲地去乙地共走了500m,途经一条宽为x m的河流,该人不小心把一件物品丢在途中,若物品掉在河里就找不到,若物品不掉在河里就能找到.已知该物品能被找到的概率为$\frac{24}{25}$,则河宽为( )
| A. | 80 m | B. | 20 m | C. | 40 m | D. | 50 m |
14.某企业节能降耗技术改造后,在生产某产品过程中几录的产量x(吨)与相应的生产能耗y(吨)的几
组对应数据如表所示:
若根据表中数据得出y关于x的线性回归方程为$\stackrel{∧}{y}$=0.7x+0.35,则表中a的值为( )
组对应数据如表所示:
| x | 3 | 4 | 5 | 6 |
| y | 2.5 | 3 | 4 | a |
| A. | 3 | B. | 3.15 | C. | 3.5 | D. | 4.5 |
4.已知函数f(x)的定义域为R,M为常数.若p:对?x∈R,都有f(x)≥M;q:M是函数f(x)的最小
值,则p是q的( )
值,则p是q的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
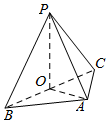 如图,在三棱锥P-ABC中,△PAB和△PAC均为边长是$\sqrt{2}$的正三角形,且∠BAC=90°,O为BC的中点.
如图,在三棱锥P-ABC中,△PAB和△PAC均为边长是$\sqrt{2}$的正三角形,且∠BAC=90°,O为BC的中点.