题目内容
下列正确结论的序号是 .
①连续函数f(x)在区间(a,b)上有零点的充要条件为f(a)•f(b)<0;
②若函数y=f(x)的图象在点M(1,f(1))处的切线方程是y=
x+2,则f(1)+f′(1)=3;
③对?x>0,不等式2x+
-a>0恒成立,则实数a的取值范围为(-∞,2);
④若f(x)=x5+x4+x3+2x+1,则f(2)的值用二进制表示为111101.
①连续函数f(x)在区间(a,b)上有零点的充要条件为f(a)•f(b)<0;
②若函数y=f(x)的图象在点M(1,f(1))处的切线方程是y=
| 1 |
| 2 |
③对?x>0,不等式2x+
| 1 |
| 2x |
④若f(x)=x5+x4+x3+2x+1,则f(2)的值用二进制表示为111101.
考点:命题的真假判断与应用
专题:函数的性质及应用
分析:①,举例说明连续函数f(x)=x2-3x+2=(x-1)(x-2)在区间(0,4)上有两个零点,但f(0)•f(4)>0,可判断①;
②,依题意,可知f′(1)=
,f(1)=
×1+2=
,从而可判断②;
③,对?x>0,不等式2x+
-a>0恒成立?a<(2x+
)min,而当x>0时,2x+
无最小值,从而可判断③;
④,用二进制表示为111101,与f(2)=25+24+23+2×2+0×21+1比较即可判断④.
②,依题意,可知f′(1)=
| 1 |
| 2 |
| 1 |
| 2 |
| 5 |
| 2 |
③,对?x>0,不等式2x+
| 1 |
| 2x |
| 1 |
| 2x |
| 1 |
| 2x |
④,用二进制表示为111101,与f(2)=25+24+23+2×2+0×21+1比较即可判断④.
解答:
解:对于①,连续函数f(x)在区间(a,b)上有零点不能得出f(a)•f(b)<0,如f(x)=x2-3x+2=(x-1)(x-2)在区间(0,4)上有两个零点,但f(0)•f(4)>0,即充分性不成立;反之,则可,故①错误;
对于②,若函数y=f(x)的图象在点M(1,f(1))处的切线方程是y=
x+2,
则f(1)的值与y=
x+2中,当x=1时的函数值相等,即f(1)=
×1+2=
,又f′(1)=
(为切线方程y=
x+2的斜率),故f(1)+f′(1)=3,②正确;
对于③,?x>0,不等式2x+
-a>0恒成立,则a<(2x+
)min=2,
而当x>0时,2x+
无最小值,
所以实数a的取值范围不是(-∞,2),故③错误;
对于④,因为f(x)=x5+x4+x3+2x+1,(111101)2=25+24+23+2×2+0×21+1=f(2),故④正确.
故答案为:②④.
对于②,若函数y=f(x)的图象在点M(1,f(1))处的切线方程是y=
| 1 |
| 2 |
则f(1)的值与y=
| 1 |
| 2 |
| 1 |
| 2 |
| 5 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
对于③,?x>0,不等式2x+
| 1 |
| 2x |
| 1 |
| 2x |
而当x>0时,2x+
| 1 |
| 2x |
所以实数a的取值范围不是(-∞,2),故③错误;
对于④,因为f(x)=x5+x4+x3+2x+1,(111101)2=25+24+23+2×2+0×21+1=f(2),故④正确.
故答案为:②④.
点评:本题考查命题的真假判断与应用,综合考查函数的零点、充分必要条件的概念及应用,考查导数的几何意义、二进制的应用,考查转化思想.

练习册系列答案
相关题目
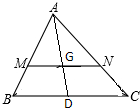 如图,△ABC中,D为BC的中点,G为AD的中点,过点G任作一直线MN,分别交AB,AC于M,N两点,若
如图,△ABC中,D为BC的中点,G为AD的中点,过点G任作一直线MN,分别交AB,AC于M,N两点,若