题目内容
若M(2,1),点C是椭圆
+
=1的右焦点,点A是椭圆的动点,则|AM|+|AC|的最小值是 .
| x2 |
| 16 |
| y2 |
| 7 |
考点:椭圆的简单性质
专题:计算题,圆锥曲线的定义、性质与方程
分析:设椭圆的左焦点为F,连接MF、AF,根据椭圆的定义得|AM|+|AC|=|AM|+(8-|AF|)=8+(|AM|-|AF|)
当M、A、F三点共线,且A在FM延长线上时,|AM|-|AF|取得最小值.利用两点之间距离公式,则不难求出这个最小值.
当M、A、F三点共线,且A在FM延长线上时,|AM|-|AF|取得最小值.利用两点之间距离公式,则不难求出这个最小值.
解答:
解:设椭圆的左焦点为F(-3,0),连接MF、AF,
∵点A在椭圆
+
=1上运动,
∴|AC|+|AF|=2a=8,
由此可得|AM|+|AC|=|AM|+(8-|AF|)=8+(|AM|-|AF|)
当M、A、F三点共线,且A在FM延长线上时,|AM|-|AF|取得最小值.
∴|AM|-|AF|的最小值为:-|MF|=-
=-
.
由此可得|AM|+|AC|的最小值为8-
.
故答案为:8-
.
∵点A在椭圆
| x2 |
| 16 |
| y2 |
| 7 |
∴|AC|+|AF|=2a=8,
由此可得|AM|+|AC|=|AM|+(8-|AF|)=8+(|AM|-|AF|)
当M、A、F三点共线,且A在FM延长线上时,|AM|-|AF|取得最小值.
∴|AM|-|AF|的最小值为:-|MF|=-
| (2+3)2+(1-0)2 |
| 26 |
由此可得|AM|+|AC|的最小值为8-
| 26 |
故答案为:8-
| 26 |
点评:本题给出椭圆内部一点和椭圆上动点,求距离之和的最小值,着重考查了椭圆的标准方程和简单几何性质等知识,属于中档题.

练习册系列答案
相关题目

 如图所示的是某单位的男职工进行健康体检时的体重情况的频率分布直方图,已知图中从左到右的前3个小组的频率之比为1:2:3,其中第2小组的频数为24,那么该单位共有男职工的人数为( )
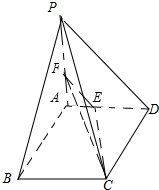
如图所示的是某单位的男职工进行健康体检时的体重情况的频率分布直方图,已知图中从左到右的前3个小组的频率之比为1:2:3,其中第2小组的频数为24,那么该单位共有男职工的人数为( )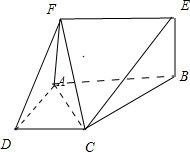 已知平面ABEF⊥平面ABCD、长方形ABEF,∠DAB=90°,AB∥CD,AD=AF=CD=2,AB=4
已知平面ABEF⊥平面ABCD、长方形ABEF,∠DAB=90°,AB∥CD,AD=AF=CD=2,AB=4