题目内容
2.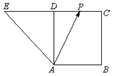 如图,四边形ABCD是正方形,延长CD至E,使得DE=CD,若点P为CD的中点,且$\overrightarrow{AP}=λ\overrightarrow{AB}+μ\overrightarrow{AE}$,则λ+μ=( )
如图,四边形ABCD是正方形,延长CD至E,使得DE=CD,若点P为CD的中点,且$\overrightarrow{AP}=λ\overrightarrow{AB}+μ\overrightarrow{AE}$,则λ+μ=( )| A. | 3 | B. | $\frac{5}{2}$ | C. | 2 | D. | 1 |
分析 建立如图所示的直角坐标系,设正方形的边长为1,可以得到$\overrightarrow{AP}=λ\overrightarrow{AB}+μ\overrightarrow{AE}$的坐标表示,进而得到答案.
解答  解:由题意,设正方形的边长为1,建立坐标系如图,
解:由题意,设正方形的边长为1,建立坐标系如图,
则B(1,0),E(-1,1),
∴$\overrightarrow{AB}$=(1,0),$\overrightarrow{AE}$=(-1,1),
∵$\overrightarrow{AP}=λ\overrightarrow{AB}+μ\overrightarrow{AE}$=(λ-μ,μ),
又∵P是点P为CD的中点,
∴$\overrightarrow{AP}$=($\frac{1}{2}$,1),
∴$\left\{\begin{array}{l}{λ-μ=\frac{1}{2}}\\{μ=1}\end{array}\right.$,
∴λ=$\frac{3}{2}$,μ=1,
∴λ+μ=$\frac{5}{2}$,
故选:B
点评 本题考查的知识点是向量在几何中的应用,向量加减的几何意义,数形结合思想,难度中档.

练习册系列答案
相关题目
10.某校高三年级有男生220人,学籍编号1,2,…,220;女生380人,学籍编号221,222,…,600.为了解学生学习的心理状态,按学籍编号采用系统抽样的方法从这600名学生中抽取10人进行问卷调查(第一组采用简单随机抽样,抽到的号码为10),然后再从这10位学生中随机抽取3人座谈,则3人中既有男生又有女生的概率是( )
| A. | $\frac{1}{5}$ | B. | $\frac{3}{10}$ | C. | $\frac{7}{10}$ | D. | $\frac{4}{5}$ |
11.“|x-1|<2成立”是“x(x-3)<0成立”的( )
| A. | 充分必要条件 | B. | 充分而不必要条件 | ||
| C. | 必要而不充分条件 | D. | 既不充分也不必要条件 |
17.函数f(x)=ln(ex+1)-$\frac{x}{2}$( )
| A. | 是偶函数,但不是奇函数 | B. | 是奇函数,但不是偶函数 | ||
| C. | 既是奇函数,又是偶函数 | D. | 既不是奇函数,也不是偶函数 |
14.${∫}_{1}^{e}$(x+$\frac{1}{x}$)dx=( )
| A. | e2 | B. | $\frac{{e}^{2}+1}{2}$ | C. | $\frac{{e}^{2}-1}{2}$ | D. | $\frac{{e}^{2}+3}{2}$ |