题目内容
4.对于函数f(x)=x图象上的任一点M,在函数g(x)=lnx上都存在点N(x0,y0),使$\overrightarrow{OM}•\overrightarrow{ON}=0(O$是坐标原点),则x0必然在下面哪个区间内?( )| A. | $(\frac{1}{e^3},\frac{1}{e^2})$ | B. | $(\frac{1}{e^2},\frac{1}{e})$ | C. | $(\frac{1}{e},\frac{1}{{\sqrt{e}}})$ | D. | $(\frac{1}{{\sqrt{e}}},1)$ |
分析 问题转化为x0是函数h(x)=x+lnx的零点,根据函数的零点的判断定理求出x0的范围即可.
解答 解:由题意得:$\frac{{y}_{0}}{{x}_{0}}$=$\frac{l{nx}_{0}}{{x}_{0}}$=-1,
即lnx0+x0=0,
即x0是函数h(x)=x+lnx的零点,
由h(x)在(0,+∞)是连续的递增函数,
且h($\frac{1}{e}$)=-1+$\frac{1}{e}$<0,h($\frac{1}{\sqrt{e}}$)=$\frac{2-\sqrt{e}}{2\sqrt{e}}$>0,
得h(x)在($\frac{1}{e}$,$\frac{1}{\sqrt{e}}$)有零点,
即x0∈($\frac{1}{e}$,$\frac{1}{\sqrt{e}}$),
故选:C.
点评 本题考查了函数零点的判断定理,考查对数函数的性质以及转化思想,是一道中档题.

练习册系列答案
 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案
相关题目
14.过点P(0,-1)的直线与抛物线x2=-2y公共点的个数为( )
| A. | 0 | B. | 1 | C. | 2 | D. | 1或2 |
12.已知圆心为(2,0)的圆C与直线y=x相切,求切点到原点的距离( )
| A. | 1 | B. | $\sqrt{2}$ | C. | 2 | D. | $\sqrt{3}$ |
16.在各项为正实数的等差数列{an}中,其前2016项的和S2016=1008,则$\frac{1}{{{a_{1001}}}}+\frac{9}{{{a_{1016}}}}$的最小值为( )
| A. | 12 | B. | 16 | C. | $\frac{1}{84}$ | D. | $\frac{2}{251}$ |
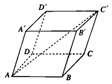 如图,在平行六面体ABCD-A'B'C'D'中,$AB=3,AD=4,AA'=4,∠BAD=\frac{π}{2}$,$∠BAA'=\frac{π}{3}$,$∠DAA'=\frac{π}{3}$,则AC'=$\sqrt{69}$.
如图,在平行六面体ABCD-A'B'C'D'中,$AB=3,AD=4,AA'=4,∠BAD=\frac{π}{2}$,$∠BAA'=\frac{π}{3}$,$∠DAA'=\frac{π}{3}$,则AC'=$\sqrt{69}$.