题目内容
13.已知A(5,-1),B(m,m),C(2,3)三点.(1)若AB⊥BC,求m的值;
(2)求线段AC的中垂线方程.
分析 (1)若AB⊥BC,则斜率的积定义-1,即可求m的值;
(2)求出中垂线的斜率,AC的中点,即可求线段AC的中垂线方程.
解答 解:(1)${k_{AB}}=\frac{m+1}{m-5}$,${k_{BC}}=\frac{3-m}{2-m}$…(2分)
${k_{AB}}×{k_{BC}}=-1⇒m=1或m=\frac{7}{2}$…(5分)
(2)${k_{CA}}=\frac{-1-3}{5-2}=-\frac{4}{3}$…(6分)
中垂线的斜率$k=\frac{3}{4}$…(7分)
AC的中点是($\frac{7}{2},1$) …(8分)
中垂线的方徎是$y-1=\frac{3}{4}(x-\frac{7}{2})$
化为6x-8y-13=0…(10分)
点评 本题考查直线方程,考查斜率的计算,属于中档题.

练习册系列答案
 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案
相关题目
4.对于函数f(x)=x图象上的任一点M,在函数g(x)=lnx上都存在点N(x0,y0),使$\overrightarrow{OM}•\overrightarrow{ON}=0(O$是坐标原点),则x0必然在下面哪个区间内?( )
| A. | $(\frac{1}{e^3},\frac{1}{e^2})$ | B. | $(\frac{1}{e^2},\frac{1}{e})$ | C. | $(\frac{1}{e},\frac{1}{{\sqrt{e}}})$ | D. | $(\frac{1}{{\sqrt{e}}},1)$ |
1.对凯里一中高二(1)、高二(2)、高二(3)、高二(4)、高二(5)五个班级调查了解,统计出这五个班级课余参加书法兴趣小组并获校级奖的人数,得出如表:
从表中看出,班级代号x与获奖人数y线性相关.
(1)求y关于x的线性回归方程$\widehaty=\widehatbx+\widehata$;
(2)从以上班级随机选出两个班级,求至少有一个班级获奖人数超过3人的概率.
(附:参考公式:$\widehatb=\frac{{\sum_{i=1}^n{({x_i}-\overline x)({y_i}-\overline y)}}}{{\sum_{i=1}^n{{{({x_i}-\overline x)}^2}}}}=\frac{{\sum_{i=1}^n{{x_i}{y_i}-n\overline x\overline y}}}{{\sum_{i=1}^n{x_i^2-n{{\overline x}^2}}}}$,$\widehata=\overline y-\widehatb\overline x$).
| 班级 | 高二(1) | 高二(2) | 高二(3) | 高二(4) | 高二(5) |
| 班级代号x | 1 | 2 | 3 | 4 | 5 |
| 获奖人数y | 5 | 4 | 2 | 3 | 1 |
(1)求y关于x的线性回归方程$\widehaty=\widehatbx+\widehata$;
(2)从以上班级随机选出两个班级,求至少有一个班级获奖人数超过3人的概率.
(附:参考公式:$\widehatb=\frac{{\sum_{i=1}^n{({x_i}-\overline x)({y_i}-\overline y)}}}{{\sum_{i=1}^n{{{({x_i}-\overline x)}^2}}}}=\frac{{\sum_{i=1}^n{{x_i}{y_i}-n\overline x\overline y}}}{{\sum_{i=1}^n{x_i^2-n{{\overline x}^2}}}}$,$\widehata=\overline y-\widehatb\overline x$).
8.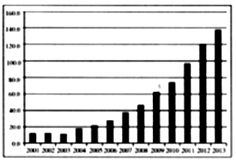 2001年至2013年北京市电影放映场次的情况如图所示.下列函数模型中,最不合适近似描述这13年间电影放映场次逐年变化规律的是( )
2001年至2013年北京市电影放映场次的情况如图所示.下列函数模型中,最不合适近似描述这13年间电影放映场次逐年变化规律的是( )
 2001年至2013年北京市电影放映场次的情况如图所示.下列函数模型中,最不合适近似描述这13年间电影放映场次逐年变化规律的是( )
2001年至2013年北京市电影放映场次的情况如图所示.下列函数模型中,最不合适近似描述这13年间电影放映场次逐年变化规律的是( )| A. | y=ax2+bx+c | B. | y=aex+b | C. | y=aax+b | D. | y=alnx+b |
18.一动圆与两圆:x2+y2=1和x2+y2-6x+5=0都外切,则动圆圆心的轨迹为( )
| A. | 抛物线 | B. | 双曲线 | C. | 双曲线的一支 | D. | 椭圆 |
18.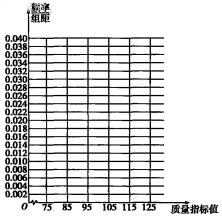 从某企业生产的某种产品中随机抽取100件,测量这些产品的某项质量指标,由测量结果得到如下频数分布表:
从某企业生产的某种产品中随机抽取100件,测量这些产品的某项质量指标,由测量结果得到如下频数分布表:
(1)在图中作出这些数据的频率分布直方图;
(2)估计这种产品质量指标值的平均数、中位数(保留2位小数);
(3)根据以上抽样调査数据,能否认为该企业生产的这种产品符合“质量指标值不低于95的产品至少要占全部产品的80%”的规定?
 从某企业生产的某种产品中随机抽取100件,测量这些产品的某项质量指标,由测量结果得到如下频数分布表:
从某企业生产的某种产品中随机抽取100件,测量这些产品的某项质量指标,由测量结果得到如下频数分布表:| 质量指标值分组 | [75,85) | [85,95) | [95,105) | [105,115) | [115,125) |
| 频数 | 6 | 26 | 38 | 22 | 8 |
(2)估计这种产品质量指标值的平均数、中位数(保留2位小数);
(3)根据以上抽样调査数据,能否认为该企业生产的这种产品符合“质量指标值不低于95的产品至少要占全部产品的80%”的规定?
 已知三棱锥A-BCD的四个顶点A、B、C、D都在球O的表面上,AC⊥平面BCD,BC⊥CD,且AC=$\sqrt{3}$,BC=2,CD=$\sqrt{5}$,则球O的表面积为12π.
已知三棱锥A-BCD的四个顶点A、B、C、D都在球O的表面上,AC⊥平面BCD,BC⊥CD,且AC=$\sqrt{3}$,BC=2,CD=$\sqrt{5}$,则球O的表面积为12π.