题目内容
袋中装有黑球和白球共7个,从中任取2个球都是白球的概率为
,现有甲、乙两人从袋中轮流摸取1球,甲先取,乙后取,然后甲再取…取后不放回,直到两人中有一人取到白球时而终止.每个球在每一次被取到的机会是等可能的.则甲取到白球的概率是 .
| 1 |
| 7 |
考点:古典概型及其概率计算公式
专题:概率与统计
分析:首先根据题意,设袋中原有n个白球,由题意知
=
,可以求出黑球有4个,白球有3个;然后根据由甲先取,可得甲有可能在第一次,第三次,第五次取到白球,据此分别求出甲在第一次,第三次,第五次取到白球的概率是多少,最后相加,求出甲取到白球的概率是多少即可.
| 1 |
| 7 |
| ||
|
解答:
解:设袋中原有n个白球,
由题意知
=
=
=
整理,得n2-n-6=0,
解得n=3或n=-2(舍去)
所以袋子中黑球有4个,白球有3个;
因此最多取4+1=5次,两人中有一人取到白球,
甲先取,甲有可能在第一次,第三次,第五次取到白球,
设甲取到白球为事件A,
则P(A)=
+
+
=
+
+
=
故答案为:
.
由题意知
| 1 |
| 7 |
| ||
|
| ||
|
| n(n-1) |
| 7×6 |
整理,得n2-n-6=0,
解得n=3或n=-2(舍去)
所以袋子中黑球有4个,白球有3个;
因此最多取4+1=5次,两人中有一人取到白球,
甲先取,甲有可能在第一次,第三次,第五次取到白球,
设甲取到白球为事件A,
则P(A)=
| 3 |
| 7 |
| 4×3×3 |
| 7×6×5 |
| 4×3×2×1×3 |
| 7×6×5×4×3 |
=
| 3 |
| 7 |
| 6 |
| 35 |
| 1 |
| 35 |
=
| 22 |
| 35 |
故答案为:
| 22 |
| 35 |
点评:本题主要考查了概率的求法,考查了学生的分析推理能力,考查了学生的运算能力,属于中档题,在历年高考中都是必考题型,解答此题的关键是首先根据题意,分别求出黑球、白球的个数是多少.

练习册系列答案
 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案
相关题目
若α是第二象限角,sin
=
,则sinα=( )
| α |
| 2 |
| 4 |
| 5 |
A、
| ||
B、
| ||
C、
| ||
D、-
|
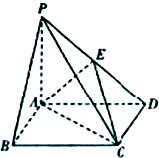 在四棱锥P-ABCD中,底面ABCD是矩形,PA=AD=4,AB=2,PB=2
在四棱锥P-ABCD中,底面ABCD是矩形,PA=AD=4,AB=2,PB=2 如图,在平面直角坐标系xOy中,钝角α的终边与单位圆交于B点,且点B的纵坐标为
如图,在平面直角坐标系xOy中,钝角α的终边与单位圆交于B点,且点B的纵坐标为