题目内容
已知数列{an}中,a1=1,anan+1=(
)n,(n∈N*)
(1)求a1,a2,a3,a4
(2)求证:数列{a2n}与{a2n-1}(n∈N*)都是等比数列.
| 1 |
| 2 |
(1)求a1,a2,a3,a4
(2)求证:数列{a2n}与{a2n-1}(n∈N*)都是等比数列.
考点:等比数列的性质,数列递推式
专题:计算题,等差数列与等比数列
分析:(1)利用数列{an}中,a1=1,anan+1=(
)n,可求a1,a2,a3,a4;
(2)由anan+1=(
)n,可得
=
,根据等比数列的定义判定出数列{a2n}与{a2n-1}(n∈N*)都是等比数列.
| 1 |
| 2 |
(2)由anan+1=(
| 1 |
| 2 |
| an+2 |
| an |
| 1 |
| 2 |
解答:
(1)解:∵数列{an}中,a1=1,anan+1=(
)n,
∴a1=1,a2=
,a3=
,a4=
;
(2)证明:∵anan+1=(
)n,
∴
=
,
∴数列a1,a3,…a2n-1,是以1为首项,
为公比的等比数列;
数列a2,a4,…,a2n,是以
为首项,
为公比的等比数列.
| 1 |
| 2 |
∴a1=1,a2=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 4 |
(2)证明:∵anan+1=(
| 1 |
| 2 |
∴
| an+2 |
| an |
| 1 |
| 2 |
∴数列a1,a3,…a2n-1,是以1为首项,
| 1 |
| 2 |
数列a2,a4,…,a2n,是以
| 1 |
| 2 |
| 1 |
| 2 |
点评:本题主要考查了等比关系的确定.解题的关键是对等比数列基础知识点的熟练掌握.

练习册系列答案
相关题目
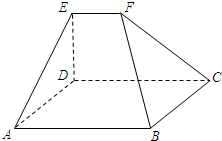 如图,在五面体ABCDEF中,四边形ABCD是矩形,DE⊥平面ABCD.
如图,在五面体ABCDEF中,四边形ABCD是矩形,DE⊥平面ABCD.