题目内容
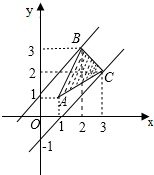
在直角坐标系xOy中，已知点A（1，1），B（2，3），C（3，2），点P（x，y）在△ABC三边围成的区域（含边界）上．
（Ⅰ）若
+
+
=
，求|
|；
（Ⅱ）设
=m
+n
（m，n∈R），用x，y表示m-n，并求m-n的最大值．
（Ⅰ）若
| PA |
| PB |
| PC |
| 0 |
| OP |
（Ⅱ）设
| OP |
| AB |
| AC |
考点：平面向量的基本定理及其意义,平面向量的坐标运算
专题：平面向量及应用
分析：（Ⅰ）先根据
+
+
=
，以及各点的坐标，求出点p的坐标，再根据向量模的公式，问题得以解决；
（Ⅱ）利用向量的坐标运算，先求出
，
，再根据
=m
+n
，表示出m-n=y-x，最后结合图形，求出m-n的最小值．
| PA |
| PB |
| PC |
| 0 |
（Ⅱ）利用向量的坐标运算，先求出
| AB |
| AC |
| OP |
| AB |
| AC |
解答：
解：（Ⅰ）∵A（1，1），B（2，3），C（3，2），
+
+
=
，
∴（1-x，1-y）+（2-x，3-y）+（3-x，2-y）=0
∴3x-6=0，3y-6=0
∴x=2，y=2，
即
=（2，2）
∴|
|=
=2
（Ⅱ）∵A（1，1），B（2，3），C（3，2），
∴
=(1，2)，
=(2，1)
∵
=m
+n
，
∴（x，y）=（m+2n，2m+n）
∴x=m+2n，y=2m+n
∴m-n=y-x，
令y-x=t，由图知，当直线y=x+t过点B（2，3）时，t取得最大值1，
故m-n的最大值为1．
解：（Ⅰ）∵A（1，1），B（2，3），C（3，2），| PA |
| PB |
| PC |
| 0 |
∴（1-x，1-y）+（2-x，3-y）+（3-x，2-y）=0
∴3x-6=0，3y-6=0
∴x=2，y=2，
即
| OP |
∴|
| OP |
| 22+22 |
| 2 |
（Ⅱ）∵A（1，1），B（2，3），C（3，2），
∴
| AB |
| AC |
∵
| OP |
| AB |
| AC |
∴（x，y）=（m+2n，2m+n）
∴x=m+2n，y=2m+n
∴m-n=y-x，
令y-x=t，由图知，当直线y=x+t过点B（2，3）时，t取得最大值1，
故m-n的最大值为1．
点评：本题考查了向量的坐标运算，关键在于审清题意，属于中档题，
练习册系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
直三棱柱ABC-A1B1C1中，∠BCA=90°，M，N分别是A1B1，A1C1的中点，BC=CA=CC1，则BM与AN所成角的余弦值为（ ）
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
有6名男医生、5名女医生，从中选出2名男医生、1名女医生组成一个医疗小组，则不同的选法共有（ ）
| A、60种 | B、70种 |
| C、75种 | D、150种 |
