题目内容
已知命题：“存在x∈[1，2]，使x2+2x+a≥0”为真命题，则a的取值范围是 ．
考点：特称命题
专题：简易逻辑
分析：根据特称命题的真假关系即可得到结论．
解答：
解：若存在x∈[1，2]，使x2+2x+a≥0，
则等价为存在x∈[1，2]，使x2+2x≥-a，
当存在x∈[1，2]时，设y=x2+2x=（x+1）2-1，
则3≤y≤8，
∴要使x2+2x≥-a，
则8≥-a，即a≥-8，
故答案为：[-8，+∞）
则等价为存在x∈[1，2]，使x2+2x≥-a，
当存在x∈[1，2]时，设y=x2+2x=（x+1）2-1，
则3≤y≤8，
∴要使x2+2x≥-a，
则8≥-a，即a≥-8，
故答案为：[-8，+∞）
点评：本题主要考查特称命题的应用，利用二次函数的性质是解决本题的关键．
练习册系列答案
相关题目
若F1、F2分别是椭圆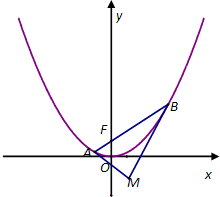
如图示：已知抛物线C：x2=4y的焦点为F，过点F作直线l交抛物线C于A、B两点，经过A、B两点分别作抛物线C的切线l1、l2，切线l1与l2相交于点M．
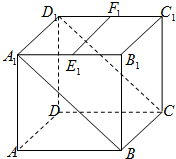如图，A1B1C1D-ABCD为边长为a的正方体，E，F分别是A1B1，C1D的中点，过EF作正方体截面，若截面平行于平面A1BCD1，则截面的面积为如图所示的程序框图，如果输入m=225，n=135，那么输出的值为（ ）
| A、45 | B、5 | C、15 | D、90 |