题目内容
已知函数f(x)=ax2+bx+
与直线y=x相切于点A(1,1),若对任意x∈[1,9],不等式f(x-t)≤x恒成立,则所有满足条件的实数t组成的集合为 .
| 1 |
| 4 |
考点:利用导数研究曲线上某点切线方程
专题:计算题,导数的概念及应用,不等式的解法及应用
分析:求出函数的导数,求出切线的斜率,由切线方程得到a,b的方程,即可得到f(x)的表达式,则不等式f(x-t)≤x即为
(x-t+1)2≤x,由于任意的x∈[1,9],则有|x-t+1|≤2
,即有-2
-x≤1-t≤2
-x,
分别求出两边的最值,令1-t不大于最小值且不小于最大值,解出即可得到.
| 1 |
| 4 |
| x |
| x |
| x |
分别求出两边的最值,令1-t不大于最小值且不小于最大值,解出即可得到.
解答:
解:函数f(x)=ax2+bx+
的导数为f′(x)=2ax+b,
由于函数f(x)=ax2+bx+
与直线y=x相切于点A(1,1),
则2a+b=1,且a+b+
=1,解得a=
,b=
,
即有f(x)=
x2+
x+
即为f(x)=
(x+1)2,
不等式f(x-t)≤x即为
(x-t+1)2≤x,
由于任意的x∈[1,9],则有|x-t+1|≤2
,
即有-2
-x≤1-t≤2
-x,
令
=m∈[1,3],则2
-x=2m-m2=-(m-1)2+1∈[-3,1],
-2
-x=-2m-m2=-(m+1)2+1∈[-15,-3],
则有-3≤1-t≤-3,即有1-t=-3,即t=4.
故答案为:{4}
| 1 |
| 4 |
由于函数f(x)=ax2+bx+
| 1 |
| 4 |
则2a+b=1,且a+b+
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 2 |
即有f(x)=
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 4 |
不等式f(x-t)≤x即为
| 1 |
| 4 |
由于任意的x∈[1,9],则有|x-t+1|≤2
| x |
即有-2
| x |
| x |
令
| x |
| x |
-2
| x |
则有-3≤1-t≤-3,即有1-t=-3,即t=4.
故答案为:{4}
点评:本题考查导数的运用:求切线方程,考查不等式的恒成立问题转化为求函数最值问题,注意运用参数分离,属于中档题.

练习册系列答案
相关题目
已知f(x)是偶函数,且x>0时,f(x)=x2+ax,若f(-1)=2,则f(2)的值是( )
| A、-1 | B、1 | C、3 | D、6 |

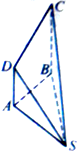 如图,在四棱锥S-ABCD中,DA⊥平面SAB,BC⊥平面SAB,AB=BC=SA=2AD=2,∠BAS=120°.
如图,在四棱锥S-ABCD中,DA⊥平面SAB,BC⊥平面SAB,AB=BC=SA=2AD=2,∠BAS=120°.