题目内容

求值：cos
π
7
cos
2π
7
cos
3π
7
cos
4π
7
cos
5π
7
cos
6π
7
=
 
．
考点：二倍角的正弦
专题：三角函数的求值
分析：由诱导公式，先计算cos
2π
7
cos
4π
7
cos
6π
7
=
1
8
，再计算cos
π
7
cos
3π
7
cos
5π
7
=-
1
8
则原式=-
1
64
．
解答： 解：由诱导公式可得：cos
6π
7
=-cos
π
7
，cos
π
7
=-cos
6π
7
，cos
3π
7
=-cos
4π
7
，cos
5π
7
=-cos
2π
7

∴cos
2π
7
cos
4π
7
cos
6π
7
=-cos
π
7
cos
2π
7
cos
4π
7
=-sin
π
7
cos
π
7
cos
2π
7
cos
4π
7
÷sin
π
7
=-
1
2
•sin
2π
7
cos
2π
7
cos
4π
7
÷sin
π
7
=-
1
4
•sin
4π
7
cos
4π
7
÷sin
π
7
=-
1
8
•sin
8π
7
÷sin
π
7
=-
1
8
•（-sin
π
7
）÷sin
π
7

=
1
8
，
而cos
π
7
cos
3π
7
cos
5π
7

=（-cos
6π
7
）（-cos
4π
7
）（-cos
2π
7
）
=-cos
2π
7
cos
4π
7
cos
6π
7

=-
1
8
，
∴原式=-
1
64
．
点评：本题主要考察了二倍角的正弦公式的应用，注意寻找解题规律，属于基础题．
练习册系列答案
相关题目
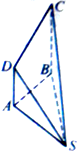如图，在四棱锥S-ABCD中，DA⊥平面SAB，BC⊥平面SAB，AB=BC=SA=2AD=2，∠BAS=120°．
（1）求证：平面SCD⊥平面SBC；
（2）求平面SAD与平面SBC所成锐角二面角的余弦值．
解不等式：(1-
3
4
)x≤
1
100
．
函数y=-2-x-2的图象经过
 
象限．
有下列命题：
①函数y=cos（x-
π
4
）cos（x+
π
4
）的图象中，相邻两个对称中心的距离为π；
②函数y=
x+3
x-1
的图象关于点（1，1）对称；
③关于x的方程ax2-2ax-1=0有且仅有一个零点，则实数a=-1；
④已知命题p：对任意的x＞1，都有sinx≤1，则?p：存在x≤1，使得sinx＞1．
其中所有真命题的序号是（　　）
A、①②B、②③C、③④D、②③④
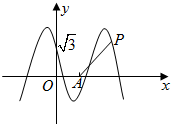如图，函数y=2cos（ωx+θ）（x∈R，ω＞0，0＜θ＜
π
2
）的图象与y轴相交于点（0，
3
），且该函数的最小正周期为π．
（Ⅰ） 求θ和ω的值；
（Ⅱ）若x∈[0，π]，求已知函数的单调递减区间．
（Ⅲ）已知点A（
π
2
，0），点P是该函数图象上一点，Q（x0，y0）是PA的中点，当y0=
3
2
，x0∈[
π
2
，π]时，求x0的值．
f（x）=
k-2x
1+k•2x
在定义域上为奇函数，则实数k=
 
．
求下列函数的值域：
（1）y=
x
+1；                       
（2）y=
1-x2
1+x2
；
（3）y=-x2+4x-7，x∈{0，1，2，3，4}；      
（4）y=-x2+4x-7（x∈[0，3]）
在△ABC中，a，b，c分别是角A，B，C所对的边，若acos2
C
2
+ccos2
A
2
=
3b
2
，求证：a+c=2b．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网