题目内容
已知双曲线
-
=1(a>0,b>0)的离心率为2,直线x=
与双曲线的两条渐近线分别交于A、B两点(A在B的上方),P是C上任意一点,
=λ
+μ
(λ、μ∈R),则λμ=( )
| x2 |
| a2 |
| y2 |
| b2 |
| a2 |
| c |
| OP |
| OA |
| OB |
A、
| ||
| B、1 | ||
| C、2 | ||
D、
|
考点:双曲线的简单性质
专题:计算题,圆锥曲线中的最值与范围问题
分析:由题意可得c=2a,从而化简3x2-y2=3a2,A(
,
a),B(
,-
a),P(
(λ+μ),
(λ-μ)a);代入即可求出.
| a |
| 2 |
| 1 |
| 2 |
| 3 |
| a |
| 2 |
| 1 |
| 2 |
| 3 |
| a |
| 2 |
| ||
| 2 |
解答:
解:由题意可得,
=2,
故c=2a,
故双曲线
-
=1可化为3x2-y2=3a2,
渐近线方程为
x±y=0,
直线x=
=
,
故A(
,
a),B(
,-
a),
则由
=λ
+μ
可得,
P(
(λ+μ),
(λ-μ)a);
则3(
(λ+μ)a)2-(
(λ-μ)a)2=3a2,
解得,λμ=1.
故选B.
| c |
| a |
故c=2a,
故双曲线
| x2 |
| a2 |
| y2 |
| b2 |
渐近线方程为
| 3 |
直线x=
| a2 |
| c |
| a |
| 2 |
故A(
| a |
| 2 |
| 1 |
| 2 |
| 3 |
| a |
| 2 |
| 1 |
| 2 |
| 3 |
则由
| OP |
| OA |
| OB |
P(
| a |
| 2 |
| ||
| 2 |
则3(
| a |
| 2 |
| ||
| 2 |
解得,λμ=1.
故选B.
点评:本题考查了圆锥曲线的定义及应用,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
下列函数中,在定义域内既是奇函数,又是增函数是( )
| A、y=sinx |
| B、y=x3-x |
| C、y=2x |
| D、y=x3 |
等比数列{an}的前n项和为Sn,若S2014=3(a1+a3+a5+…+a2013),a1a2a3=8,则log2a2014的值为( )
| A、2012 | B、2013 |
| C、2014 | D、无法确定 |
已知P为椭圆
+
=1上的点,F1、F2为其两焦点,则使∠F1PF2=90°的点P有( )
| x2 |
| 16 |
| y2 |
| 12 |
| A、4个 | B、2个 | C、1个 | D、0个 |
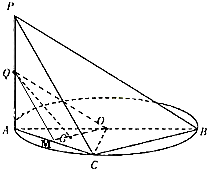 如图,AB是圆O的直径,PA垂直圆O所在的平面,C是圆O上的点.
如图,AB是圆O的直径,PA垂直圆O所在的平面,C是圆O上的点.