题目内容
18.已知f(x)=$\frac{1}{1+x}$.(1)解不等式f(|x|)>|f(2x)|;
(2)若0<x1<1,x2=f(x1),x3=f(x2),求证:$\frac{1}{3}$|x2-x1|<|x3-x2|<$\frac{1}{2}$|x2-x1|.
分析 (1)对x的范围进行讨论,去绝对值符号解出;
(2)用x1,x2表示出|x3-x2|,求出(1+x1)(1+x2)的范围即可得出结论.
解答 解:(1)∵f(|x|)>|f(2x)|,即$\frac{1}{1+|x|}$>|$\frac{1}{1+2x}$|,即$\left\{\begin{array}{l}{1+|x|<|1+2x|}\\{x≠-\frac{1}{2}}\end{array}\right.$,
当x≥0时,不等式为1+x<1+2x,解得x>0;
当-$\frac{1}{2}$<x<0时,不等式为1-x<1+2x,解得x>0(舍);
当x<-$\frac{1}{2}$时,不等式为1-x<-1-2x,解得x<-2.
综上可知,不等式f(|x|)>|f(2x)|的解集为(-∞,-2)∪(0,+∞).
(2)证明:∵0<x1<1,∴x2=f(x1)=$\frac{1}{1+{x}_{1}}$>$\frac{1}{2}$.
∴|x3-x2|=|$\frac{1}{1+{x}_{2}}$-$\frac{1}{1+{x}_{1}}$|=$\frac{|{x}_{2}-{x}_{1}|}{(1+{x}_{1})(1+{x}_{2})}$,
∵(1+x1)(1+x2)=(1+x1)(1+$\frac{1}{1+{x}_{1}}$)=2+x1,
∴2<(1+x1)(1+x2)<3
∴$\frac{1}{3}$<$\frac{1}{(1+{x}_{1})(1+{x}_{2})}$<$\frac{1}{2}$,∴$\frac{1}{3}$|x2-x1|<$\frac{|{x}_{2}-{x}_{1}|}{(1+{x}_{1})(1+{x}_{2})}$<$\frac{1}{2}$|x2-x1|,
即$\frac{1}{3}$|x2-x1|<|x3-x2|<$\frac{1}{2}$|x2-x1|.
点评 本题考查了绝对值不等式的解法,不等式的性质,属于中档题.

 互动课堂系列答案
互动课堂系列答案 激活思维智能训练课时导学练系列答案
激活思维智能训练课时导学练系列答案| A. | {1} | B. | {1,2} | C. | {2,3} | D. | {1,2,3} |
| A. | $-\frac{{7\sqrt{2}}}{10}$ | B. | $-\frac{{\sqrt{2}}}{10}$ | C. | $\frac{{7\sqrt{2}}}{10}$ | D. | $\frac{{\sqrt{2}}}{10}$ |
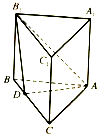 如图,在直三棱柱ABC-A1B1C1中,四边形ABB1A1是边长为$\sqrt{3}$的正方形,BC=3,D为BC上的一点,且平面ADB1⊥平面BCC1B1.
如图,在直三棱柱ABC-A1B1C1中,四边形ABB1A1是边长为$\sqrt{3}$的正方形,BC=3,D为BC上的一点,且平面ADB1⊥平面BCC1B1.