题目内容
若不等式log2(|x+1|+|x-2|-m)≥2恒成立,则实数m的取值范围为 .
考点:绝对值不等式的解法
专题:不等式的解法及应用
分析:由于不等式log2(|x+1|+|x-2|-m)≥2恒成立?|x+1|+|x-2|-m≥22,求出|x+1|+|x-2|的最小值即可.
解答:
解::∵不等式log2(|x+1|+|x-2|-m)≥2恒成立,
∴|x+1|+|x-2|-m≥22,化为|x+1|+|x-2|≥4+m,
∵|x+1|+|x-2|≥3,
∴3≥4+m,解得m≤-1.
∴实数m的取值范围为(-∞,-1],
故答案为:(-∞,-1].
∴|x+1|+|x-2|-m≥22,化为|x+1|+|x-2|≥4+m,
∵|x+1|+|x-2|≥3,
∴3≥4+m,解得m≤-1.
∴实数m的取值范围为(-∞,-1],
故答案为:(-∞,-1].
点评:本题考查了对数的运算性质、绝对值的几何意义、恒成立问题的等价转化等基础知识与基本技能方法,属于中档题.

练习册系列答案
相关题目
一个四棱锥的三视图如图所示,则此四棱至的四个侧面中的最大面积是( )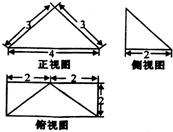

| A、3 | ||
B、2
| ||
| C、6 | ||
| D、8 |
已知复数z=i,
是z的共轭复数,则
=( )
. |
| z |
| ||
| z |
| A、1 | B、-i | C、i | D、-1 |

